Sijoituksen tuoton laskeminen

Tuoton laskeminen on taloudellisessa mielessä arvonluonnin määrän laskemista pääomalle. Pääoma on tässä tapauksessa jotain, jolla on rahallisesti mitattava arvo, joka voi tuottaa edelleen. Pääomaa ovat esimerkiksi kiinteistöt, asunnot, metsä ja arvopaperit, vaikka jokin erikoisosaaminen voidaan ajatella myös pääomana. Tuotto voidaan laskea kaikille pääomalajeille samalla perusperiaatteella. Katsotaan tuoton laskentaa esimerkkien kautta.

Tuottoa pääomalle

Tuottoa mitataan monilla mittareilla, kuten sijoitetun pääoman tuotto, oman pääoman tuotto tai kokonaispääoman tuotto. Keskitytään artikkelissa kuitenkin osakesijoittajan näkökulmaan, vaikka käytännössä melkein kaikki tuotot lasketaan samankaltaisesti. Perusmuotoisesti osakesijoituksen tuotto voidaan laskea:

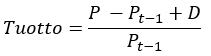
Eli sijoitusajan tuotto on alun pääoman P_t-1 ja sijoitusajan lopun pääoman P välillä ansaittu tuotto (lisättynä mahdollisella osingolla D). Tuottoprosentin saamiseksi tuotto jaetaan vielä alkupääomalla. Tuotto koostuu siten pääomatuotosta ja osinkotuotosta (sijoitusten suorituskykyä vertailtaessa osingolla oikaistu tuotto voi antaa täsmällisemmän kuvan).

Esimerkiksi sijoitetaan 1000 euroa 1 vuodeksi. Vuoden päästä pääoma on kasvanut 1100 euroon, minkä lisäksi on ansaittu 20 euroa osinkoa. Siten tuotto:

(1100 - 1000 + 20) / 1000 = 0,12 eli 12 %.

Tämä on yhden sijoitusjakson tuoton peruskaava, jota voi aina käyttää kun verrataan sijoitusajan alun ja lopun pääoman määrää tuoton määrittämiseksi. Mutta miten loppupääoma P käytännössä rakentuu, riippuu sijoituskohteesta.

Tuotto pääomalle muodostuu kahdella eri periaatteella, joko yksinkertaisella tai koronkoron periaatteella. Käytännössä sijoituksissa käytetään melkein aina koronkoron huomioivaa tapaa, koska ansaitulle tuotolle on mahdollista ansaita lisää tuottoa. 

Koronkoron tapa on tarkempi, esimerkiksi osakkeille. Yksinkertaista tapaa voi käyttää tuottoennusteiden tai odotetun tuoton laskentaan, tai velkakirjasijoituksissa, kun kuponki maksetaan vain nimellisarvolle eikä sitä sijoiteta uudelleen.

Tuottolaskenta koronkorolla

Oletetaan, että sijoittajalla on osakkeeseen sijoitettavaksi 1000 € pääoma, jolle saadaan 5 % vuosituotto. Kolmen vuoden päästä sijoituksen arvo on

• 1000 x 5 % = 50 €, joten 1. vuoden pääoma tuottoineen 1000 + 50 = 1050; 2. vuoden tuotto 1050 x 5 % = 52,5 € ja pääoma 1050+ 52,5 = 1102,5; 3. vuoden tuotto 1102,5 x 5 % = 55,1 € jolloin alkuperäinen pääoma on kasvanut 3. vuoden lopussa 1157,6 euroon. Laskenta näin on työlästä, joten lyhyemmin

• 1000 x ( 1 + 0,05 ) x ( 1 + 0,05 ) x ( 1+0,05 ) = 1157,6 €, tai vuosikorkotekijää hyödyntämällä vielä lyhyemmin

• 1000 x ( 1 + 0,05 ) ^3 = 1157,6 €, eli tuotto 1157,6 - 1000 = 157,6 €

• Jos tuotto olisi laskettu yksinkertaisella tavalla, saataisiin tuotoksi 1000 x 0,05 x 3 = 150 € ja loppupääomaksi 150 + 1000 = 1150 €.

• Aritmeettisena keskiarvona kolmen vuoden toteutunutta tuottoa (157,6 / 3 = 52,53 € tai 5,25 %) voisi hyödyntää tulevien sijoituksen odotettuna vuosituottona, mistä se on paras arvio mutta ei huomioi koronkorkoa.

• Geometrinen keskiarvo on parempi kun vertaillaan erisuuruisten pääomien tuottoja keskenään, kuten sijoitusrahastoissa. Tätä sanotaan myös oikaistuksi tuotoksi ja se huomioi korkoa korolle.

Sijoituksissa jokaisena vuotena edellisen vuoden kertyneelle pääomalle saadaan uusi tuotto. Kertynyt pääoma voi olla lopulta myös alkupääomaa pienempi, joka tietenkin tarkoittaa tappiota, eli tuotto on ollut negatiivinen. Laskentaa voidaan tarkentaa monella tapaa, kuten sisällyttämällä kuluja tai tekemällä laskenta muille aikajaksoille kuin tasavuosille. 

Esimerkin 157,6 euron tuottoa voisi sanoa myös sijoitusajan efektiiviseksi tuotoksi, tai 3 vuoden tuotoksi.

• ((1 + 0,05 ) ^3 -1) x 100 = 15,76 %, joka muunnettuna efektiiviseksi vuosituotoksi on

• ((1 + 0,1576 ) ^( 1 / 3 ) -1) x 100 = 5,00 %, eli alkuperäinen nimellinen vuosituotto on sama kuin 3 vuoden tuoton efektiivinen vuosituotto, sekä myös 3 vuoden geometrinen tuottokeskiarvo.

Tuoton kasvuvauhtiin vaikuttaa, mille aikajaksolle tuotto lasketaan eli miten usein se lasketaan pääomalle. Se voi olla päivä, kuukausi vuosi tai jokin muu korkojakso (tuottojakso). Vuosituottona

• Vuosittain ((1 + 0,05 / 1) ^1 -1) x 100 = 5,000 % (eli nimellinen vuosituotto)

• Puolivuosittain ((1 + 0,05 / 2) ^2 -1) x 100 = 5,0625 %

• Kuukausittain ((1 + 0,05 / 12) ^12 -1) x 100 = 5,1162 %

• Päivittäin ((1 + 0,05 / 365 ) ^365 -1) x 100 = 5,1267 %

• Jatkuvana (e ^0,05 -1) x 100 = 5,1271 %

Näin tuottojakso vaikuttaa todellisen vuosituoton määrään, missä huomioidaan koronkorko. Sama vaikutus toteutuu mille tahansa aikajaksolle; mitä pidempi aikajakso, sitä enemmän korkoa korolle -vaikutus näkyy.

Arvopaperituottojen laskennassa osakkeita ostetaan ja myydään päivittäin, joten korkoa korolle vaikuttaa päivätasolla. Kiinteistö- ja metsäsijoittamisessa tuotto lasketaan harvemmin, esimerkiksi vuosi-, puolivuosi-, tai vuosineljännesperusteisesti.

Lainakorkolaskut tehdään useimmiten päiväkorkoperusteisesti pääomalle, ilman koronkorkoa.

Katso myös: Miten lainan korko lasketaan?

Jatketaan 3 vuoden sijoitusesimerkkiä päivän tuottojaksoilla ja lasketaan 3 vuoden tuotto efektiivisesti huomioiden korkoa korolle: 

((1 + 0,05 / 365) ^(365 x 3) -1) x 1000 = 161,8 €

Tuoton laskenta vastaavasti esimerkiksi 170 päivän ajalle: 

((1 + 0,05 / 365) ^170 -1) x 1000 = 23,6 € efektiivisesti pääomalle 170 päivän aikana.

Laskeminen onnistuu efektiivisesti mille aikajaksolle tahansa.

Kulujen sisällyttäminen tuottoon

Oletetaan sijoitus 5 % tuotolla 1000 € pääomalle 1 vuoden aikana, josta lisäksi maksetaan kuukausittain 1 euron säilytyspalkkio. Säilytyspalkkiot ovat vuoden aikana 1 x 12 = 12 €. 

Tuotto ilman kuluja olisi 50 €, joten säilytyspalkkion huomioinnin jälkeen tuotto on 50 -12 = 38 € tai 38 / 1000 x 100 = 3,8 %.

Koska kulut olisi vähennettävä joka kuukausi kertyvästä pääomasta, voidaan tuotto laskea tuotto tarkemmin kuukausiperusteisesti 0,05 / 12 x 1000 = 4,2 €, josta vähennetään vielä 1 € säilytyspalkkio eli 1. kuukauden tuotoksi tulee 3,2 €. 12. kuukauden tuotoksi tulee 3,3 €, koska koronkorko vaikuttaa laskentaan vuotta pienemmällä tuoton laskentavälillä. Koko vuoden tuotoksi tulisi pyöreästi 39 €.

Tuottojen laskennassa huomioitavia tekijöitä on siten pääoma, tuotonlaskentaväli, sijoitusaika, osingot, kulut ja odotettu tuotto tai toteutunut tuotto. Laskentatapa on samankaltainen läpi kaikkien tuottolaskentojen, mutta laskentaa voi tarkentaa haluamallaan tavalla.

Jos tuotot koostuvat eri kokoisista rahavirroista, niin tuoton voi laskea myös sisäisen korkokannan menetelmällä, jota voi sanoa rahamääräpainotetuksi tuotoksi.

Edellä mainitut esimerkit koskivat tuoton laskemista, kun kaikki tekijät tunnetaan eli käytännössä toteutuneen tuoton laskemista.

Odotetun tuoton laskenta

Odotettu tuotto on tulevien tuottojen ennakointia, perustuen esimerkiksi historialliseen toteutuneiden tuottojen aritmeettiseen keskiarvoon, mutta se voidaan määrittää myös skenaariotodennäköisyyksillä painotettuna.

Tehdään esimerkiksi 3 skenaariota:

A) Tuotto on -5 % ja todennäköisyys 20/100,

B) Tuotto on 5 % ja todennäköisyys 50/100,

C) Tuotto on 10 % ja todennäköisyys on 30/100.

Odotettu tuotto on tuottojen ja skenaariotodennäköisyyksien tulojen summa:

• ( ( -0,05 x 0,2 ) +  ( 0,05 x 0,5 ) +( 0,1 x 0,3 ) ) x 100 = 4,5 % (todennäköisyyksien summan on oltava 1 tai 100 %).

Esimerkissä odotettu tuotto on positiivinen 4,5 %, vaikka A skenaarion tapahtuessa toteutunut tuotto on pahimmillaan negatiivinen -5 %. Skenaarioita ja niiden todennäköisyyksiä voi olla kuitenkin vaikea arvioida luotettavasti.

Odotettu tuotto voidaan laskea myös rahoitusteoreettisesti ns. CAPM-mallilla, jossa arvioitu tuleva tuotto perustuu sijoituskohteen ja markkinatuoton menneiden tuottojen muutoksien, eli volatiliteettien suhteellisten muutosten vertailuun. Tätä suhdetta kuvataan beta-kertoimella. CAPM- tuoton ja muut muuttujat voi laskea esim. pankkiasiat.fi investointilaskurilla.

Tuottojen laskenta sijoituskohteen mukaan

Rahastotuoton laskeminen

Rahaston tuoton laskeminen ei poikkea muiden arvopaperin tuottojen laskennasta, mutta tuotossa on huomioitava mahdollisia erilaisia rahastokuluja, kuten hallinnointipalkkio, merkintäpalkkio ja lunastuspalkkio. Kaikki syövät rahastosijoituksen tuottoa.

Rahaston kulujen vaikutusta tuottoon voi laskea pankkiasia.fi:n sijoituslaskurilla.

Vuokratuoton laskeminen

Vuokratuotto lasketaan myös samankaltaisesti muiden pääomatuottojen kanssa. Vuokratuotoissa on huomioitava vastikkeet, korot, tyhjät kuukaudet ja remonttikulut, jotka kaikki syövät sijoituksen tuottoa.

Vuokratuoton laskentaa voi kokeilla pankkiasiat.fi:n vuokratuottolaskurilla.

Metsätuoton laskeminen

Metsä on myös pääomaa, joten samat tuotonlaskennan periaatteet pätevät jälleen metsätuoton laskentaan. Metsän hankinnassa ostohinta vaikuttaa tuottoon erityisen voimakkaasti, sillä metsän tuotto on varsin vakaata ja rajattua alueesta riippuen.

Metsä kasvaa arvioitua vauhtia, joka on mahdollista laskea rahamääräisesti. Tuotosta on kuitenkin vähennettävä mahdolliset korjuukulut ja istutustyöt.

Arvopaperituoton laskeminen

Arvopaperituoton laskeminen on tuottolaskennan ydintä, jota yllä käytiin läpi usealla esimerkillä. Arvopapereissakin on eroja, kuten johdannaiset, velkakirjat ja osakkeet, joiden ominaispiireet on hyvä tuntea.

Johdannaisia ovat esimerkiksi futuurit, termiinit, optiot, warrantit ja sertifikaatit, jodein arvolaskenta voi poiketa osakkeen tai velkakirjan arvon laskennasta.

Tuottolaskentoja voi tehdä esimerkiksi pankkiasiat.fi:n sijoituslaskurilla, diskonttolaskurilla tai investointilaskurilla.

Tuottojen laskentaa helpottaa taulukkolaskentaohjelmat kuten excel, jossa on valmiina useita hyödyllisiä komentoja tuottolaskelmille. Lue esimerkiksi artikkeli sijoittajan hyödylliset excel-kaavat.

Katso myös:

Osakkeen hintahistoria riskin ja tuoton selittäjänä

Optimaalinen sijoitussalkku

Miten lainan korko lasketaan?

Tunnetko erilaiset korkokäsitteet?

Korkolaskuri

Lainalaskuri

Kaikki pankkiasiat.fi laskurit