Osakkeen hintahistoria riskin ja tuoton selittäjänä

Pörssinoteeratuilla osakkeilla tai arvopapereilla kertyy hintahistoriaa, jota voi hyödyntää monella tapaa esimerkiksi riski/tuottosuhteen määrittelyssä. Katsotaan millaista informaatiota menneistä hinnoista voi saada ja miten siitä voisi hyötyä.

Ensimmäiseksi hintasarjoista lasketaan usein tuotto, josta saadaan tuottohistoria. Käytetään artikkelissa esimerkkinä Nokian NYSE:ssä noteerattua osaketta, josta päivittäistä hintadataa on väliltä 1.7.1994 – 27.12.2023, eli lähes 30 vuotta. Tutkitaan taulukkolaskentaohjelmalla mitä saamme siitä irti. Artikkelissa käytetyn mallitiedoston voi ladata artikkelin lopusta.

Tuoton laskenta

Tuottojen laskennalla voidaan tarkoittaa sijoituksen pitoajan tuottoa, mutta myös arvopaperihintojen muutoksia. Tässä artikkelissa käsitellään jälkimmäisiä, mutta periaatteessa kyse on samasta asiasta, missä hintaa, tai salkun arvoa verrataan johonkin menneeseen ajankohtaan. Arvopaperin hintahistoria kertoo meille riskistä, mikä vaikuttaa myös salkun arvon laskentaan ja sen säilyttämiseen.

Ensiksi lasketaan tuotot mieluummin logaritmisina tuottoina, eli logtuottoina. Molempia voi käyttää, mutta laskemalla tuotot logtuottoina tulee niiden jakaumasta normaalijakauma (hintajakauma on taas lognormaalijakauma!) tai lähemmäs sitä, vaikka ero ei ole käytännössä liian suuri. Tuotot mittaavat absoluuttista muutosta ja logtuotot suhteellista muutosta. Logtuottojen ydin on korkoa korolle, eli kasvuvaikutuksen huomiointi, mikä on sijoittamisessa ydinasiaa. Logtuotto ikään kuin poistaa sijoittajien ylisuuret odotukset kaupankäynnissä ja on siten hieman realistisempi mittari kuin tuotto.

H_t= päivän hintanoteeraus ja H_t-1 on edellisen päivän hintanoteeraus. Ln merkitsee luonnollista logaritmia. Molemmat tuotot ovat helppoja laskea, mutta logtuotot tuovat muutakin etua, kuten summaus yli ajan ja parempi vertailtavuus eri aikajaksoilla.

Menemättä liian syvälle teoriaan, alla on artikkelin esimerkissä käytetyn Nokian NYSE-noteerauksen hintahistoria ajalta 7/1994-12/2023. 

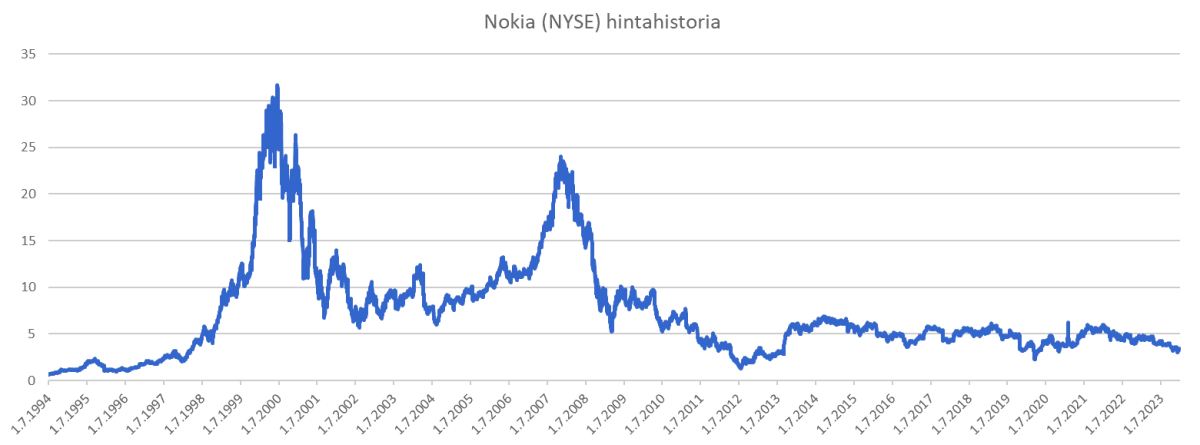
Mukana on siis vuosituhannen vaihteen "teknokuplan" hinnat ja hintapiikki ennen 2008 finanssikriisiä, sekä myös sen jälkeinen pitkä lasku. Hinnan historia ei sinänsä kerro muuta kuin millä hintavälillä kurssi on liikkunut. Hintatasoja käytetään ns. teknisessä analyysissä, eli siitä johdettujen indikaattoreiden, kuten RSI, MACD ja Fibonacci-tasojen kautta tuottamaan sijoitukselle voittoa enemmän kuin tappiota. Jatketaan osakkeen logtuottohistoriaan, joka on hyödyllisempi riskinarvioinnissa.

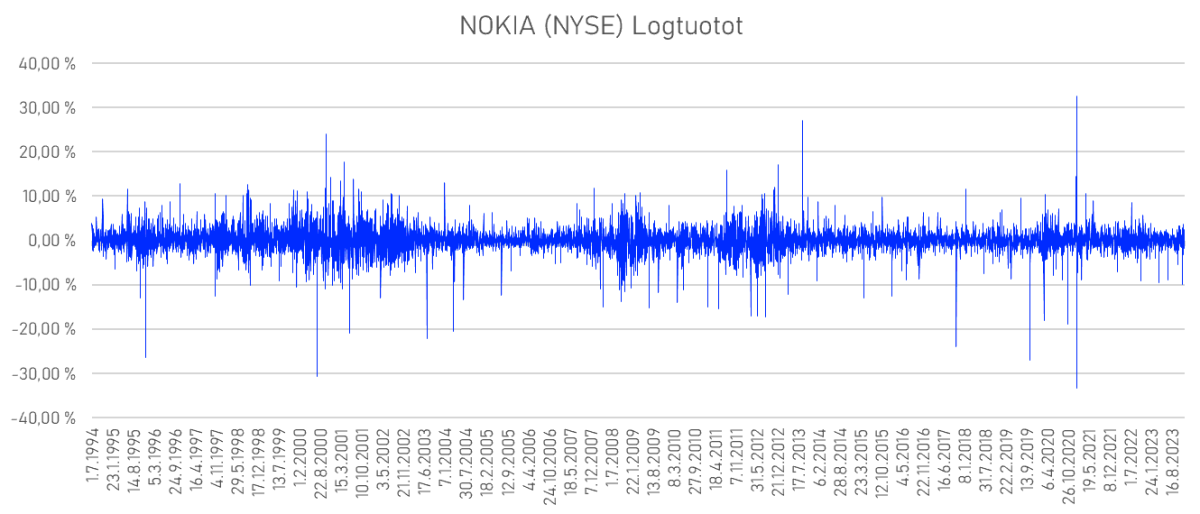
Logtuottohistoriasta näkee, että suurin osa tuotoista pyörii nollan lähistöllä ja poikkeavat piikit ovat verrattain harvinaisia, mutta ne voivat olla erittäin suuria. Missä hajontaa on enemmän (laajemmat siniset alueet), on myös volatiliteetti suurempaa mikä tunnetaan myös keskihajontana. Se on tärkeä riskimittari, sillä mitä suurempi on volatiliteetti, sitä suurempi on riski, mutta samoin voivat olla myös tuototkin. Riski/tuottosuhde onkin sijoittamisessa kenties tärkein konsepti. 

Muunnetaan logtuotot vielä jakaumiksi, josta tämä tuottojen jakautuminen nähdään vielä selvemmin. Alla on vasemmalla Nokian osakkeen tuottojakauma ja oikealla logtuottojakauma.

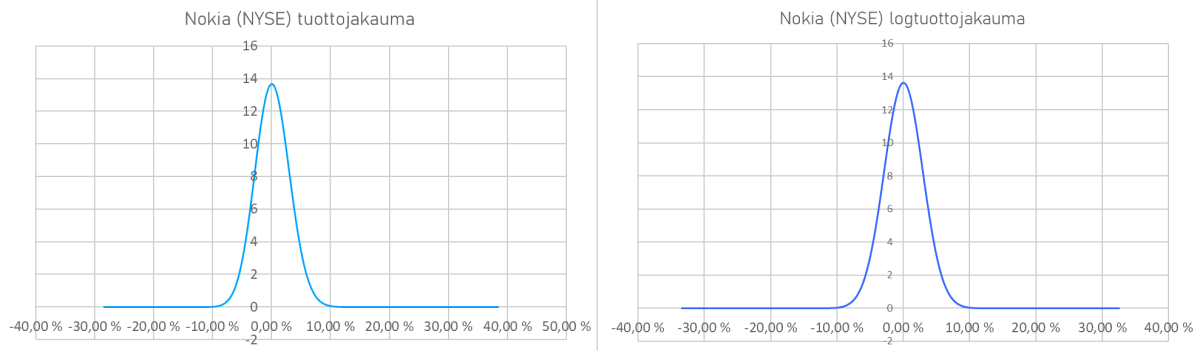
Kovin suurta eroa tässä tapauksessa ei ole silmämääräisesti tuotoilla, tai logtuotoilla. Tähän muotoon vaikuttaa paitsi osake, niin valitun hintahistorian tai -jakson pituus. Kuitenkin yleisesti tuottojakaumat (vasemmalla) eivät ole normaalijakautuneita, vaan ovat vasemmalle vinoutuneet. Kuvasta voidaan nähdä, että tuottojakauman vasen "häntä" on lyhyempi kuin oikea puoli, eli historian suurimmat päivähintamuutokset ovat olleet positiivisia lähes 40 % asti. Tämä tapahtui 27.1.2021 "meemiosakkeiden" buumin aikaan, jolloin suurin positiivinen päivämuutos oli peräti 38,5 %. Samoin negatiivisin muutos tapahtui seuraavana päivänä, 28.1.2021 jolloin kurssi laski 28,4 % lähes edellisille tasoille.

Logtuotoilla vastaavat muutokset ovat voimakkuudeltaan kokonaisuutena tasaisempia; nousu 32,6 % ja lasku 33,4 %. Tässä kannattaa huomata suurempi symmetrisyys, eli etumerkistä riippumatta tuotot ovat suuruudeltaan lähempänä kuin tavalliset tuotot. Jos jakauma ei ole normaalijakautunut, voi se aiheuttaa virheitä rahoitusmalleihin, sijoitusstrategioihin ja riskinhallintaan. Toki logtuottojakaumaa ei silti voi väittää aina normaalijakautuneeksi, mutta se on usein riittävän lähellä sitä tai lähempänä kuin tavallinen tuottojakauma.

Keskeinen raja-arvolause on merkittävä tilastollista analyysiä helpottava konsepti rahoituksessa. Sen mukaan useiden otosten, esimerkiksi tässä tuottohistoriasta poimittujen satunnaisten tuotto-otosten keskiarvot ovat normaalijakautuneita riippumatta koko populaation eli tuottohistorian jakauman muodosta. Lauseen avulla esimerkiksi pelkällä otosjakaumalla voisi kätevämmin tehdä oletuksia arvopaperin tuottojakaumasta, tai potentiaalisen usean arvopaperin salkun tuottojakaumasta ja laskea siitä riskilukuja.

Hyväksytyn riskitason määritys

Osakkeen riskiä voi mitata useammalla tavalla. Keskeinen näkökulma on siis riskin ja tuoton suhde. Usein oppikirjamaisesti suhde on noin 1:3, eli 1 osa tappioriskiä ja 3 osaa voittoa. Tappio kiinnostaa eniten ensin, koska se on osa, jossa rahaa voi hävitä. Haluamme tunnistaa ja minimoida sen, vaikka riskiä ei voikaan kokonaan poistaa.

Yksi yleinen menetelmä on laskea ns. value-at-risk, eli VaR. Se kertoo valitulla todennäköisyydellä, että tappio ei ylitä tietyllä aikajaksolla tiettyä rajaa. Esimerkiksi jos laskettu tuottodatamme on päivävälillä, niin voimme siitä laskea hyväksytyt riskitasot 1 päivän ajalle.

Todennäköisyystason voi valita halutuksi, mutta yleisiä ovat 95 %, 99 % tai rahoitusalan yrityksillä sääntelyn mukaan jopa 99,9 % tai kireämpi. Eli esimerkiksi haluamme tietää, että 95 % varmuudella 1 päivän aikana tappiomme ei ylitä tiettyä lukua. Lasketaan ensin Nokian tuottosarjasta keskiarvo ja -hajonta.

Logtuottojen keskiarvo = 0,02%

Logtuottojen keskihajonta = 2,92 %

Keskiarvo on aavistuksen positiivinen, eli keskimäärin päivätuotto on ollut 30 vuoden aikana logtuotoilla hieman positiivinen. Huomaa, että normaalijakaumassa keskiarvon tulisi olla 0 tai lähellä sitä. Olipa tuottojakauma normaali tai ei, niin historiallisen datan pohjalta lasketussa VaR-luvussa meidän ei sitä tarvitse tietää, mikä onkin yksi tämän tavan etu. Toinen on sen verrattainen yksinkertaisuus. Historiallisen VaR:in lisäksi muita tapoja ovat laskea vastaava luku ovat Varianssi-Kovarianssi- ja Monte Carlo -menetelmät.

Lasketaan päivälle maksimitappio 90, %,95 % ja 99 % todennäköisyystasolla. Yksinkertaisesti lajittelemme logtuottodatan suurimmasta pienimpään ja otamme siitä esimerkiksi 90 % kohdalla olevan arvon, kätevimmin esimerkiksi excelin PROSENTTIPISTE.SIS -funktiolla (jolloin sorttausta ei tarvitse). Saamme seuraavat arvot:

90 % todennäköisyydellä -2,84 % maksimitappio

95 % todennäköisyydellä -4,15 % maksimitappio

99 % todennäköisyydellä -7,95 % maksimitappio

Esimerkiksi 90 % todennäköisyydellä tappio 1 päivän aikana ei ole suurempi kuin 2,84 % pääomasta. Jos olisimme sijoittanut 10 000 euroa, niin tämä tarkoittaisi enintään 284 € tappiota päivässä. Historiasta voimme laskea, tätä -2,84 % negatiivisempia muutoksia on ollut 743 kpl, kun kaikkia päiviä 7424. Eli juuri se jäännös 10 %, koska määritimme 90 % luotettavuustason. Voisi myös ilmaista, että keskimäärin joka 10. kaupankäyntipäivä koemme VaR 90 % -tasoa suuremman tappion.

VaR 90 % on melko väljä ja yleisimpiä ovat kireämmät 95 %, 99 %, 99,5 % ja 99,9 %. Esimerkiksi 99 % tasolla maksimitappio ym. tavalla olisi -7,95 %. Täytyy muistaa, että datahistoria on todella pitkä, todennäköisesti tarpeettoman pitkä. Normaalisti voisi riittää viimeisin 1-3 vuoden data. Tässä tapauksessa pudottamalla Nokian datahistoria kahteen vuoteen, muuttuu jakauman muoto enemmän normaalijakauman suuntaan. Jos jakauma on normaali, voisimme käyttää taulukoituja z-arvoja hakemaan arvoja alkuperäisestä sarjasta, kuten tässä tuottosarjasta.

Esimerkiksi 90 % todennäköisyydellä standardi normaalijakauman Z-arvo = (tuotto - keskiarvo) / keskihajonta = 1,28. Samoin 95 % Z = 1,65 ja 99 % Z = 2,33. Samasta kaavasta voidaan ratkaista esimerkiksi 90 % todennäköisyyttä vastaava tuotto: Tuotto + Z-arvo x keskihajonta, eli 0,02 % + 1,28 x 2,92 % = 3,8 %. Se ei ole aivan sama kuin 2,84 % mikä kertoo että normaalijakauman oletus ei toimi tällä pitkällä datalla. Sen sijaan lyhyemmällä 2 vuoden datalla se olisi lähes sama.

Riskiä vastaava tuotto

Kun olemme laskeneet riskin, niin voimme määrittää vaadittavan tuotonkin. Otetaan yksinkertaistetuksi esimerkiksi 10 000 euron osakesalkku, jossa on vain yksi osake, em. Nokia. Useamman arvopaperin salkulle riski on mahdollista laskea melkein yhtä helposti, laskemalla ensin tuotot kaikille osakkeille ja painottamalla ne omistusten suhteessa.

90 % todennäköisyydellä -2,84 % vastaa 10 000 euron sijoituksessa 284 euron päivittäistä maksimitappiota. Usein ns. oppikirjamaiseksi esimerkiksi mainitaan 1:3 suhteen odotettu tuotto per tappio, eli 3 osaa voittoa ja 1 osaa tappiota. Näin ollen meidän tulisi saada 3 x 284 = 852 € voittoa otettua riskiä vastaan keskimäärin, kun käytetään Nokian lähes 30 vuoden historiaa.

Voisimme asettaa Stop Loss -toimeksiannon, ettei tappiomme varmasti ylitä päivän aikana 2,84 % pääomasta. On ymmärrettävä, että riski/tuottosuhde on täysin sijoittajakohtainen. Haluttu voitto riippuu sijoituskohteesta ja riskinottohalusta. Mutta pääsääntöisesti riski/tuottotason voisi määrittää tai kuvailla näin:

• Valitse osake kattavan tutkiskelun jälkeen, kuten em. tavalla katsomalla sen historiaa ja myös itse liiketoimintaa, mikä on mahdollista
• Jos maksimiriski on määritetty laskemallamme VaR-tavalla, niin selvitä mitä tuottotasoa vaaditaan ja onko se realistista.
• Jos on, niin laske riski/tuotto
• Jos se on alle riskituottorajan (esim. 1:2 eikä 1:3, eli voisimme saada voittoa vain 2 osaa emmekä 3 osaa yhtä tappio-osaa kohti)
• Jos haluttu riski/tuottotaso on liian vaikea saavuttaa, niin aloitamme alusta toisella sijoitusidealla.

Odotettua tuottoa voi laskea useilla eri tavoilla, esimerkiksi perinteisellä CAPM-mallilla, tai jollain muulla perustellulla tavalla.

Kuvitellaan, että sijoitamme osakkeeseen joka maksaa 20 euroa. Sen VaR on 2 euroa (10 %), joten riskeeraamme sen verran saavuttaaksemme voittoa. Odotamme osakkeen nousevan 26 euron tasolle lähiaikoina, joten odotettu tuottomme on 6 euroa. Riski/tuottosuhteemme on 1:3.

Entä jos haluamme ottaakin maksimissaan vain 1 euron tappion, mutta pidämme voittotavoitteen? Riskituottosuhteemme muuttuu 1:6 suhteeseen, mikä voi olla erittäin epärealistinen tavoite. Maksimitappio toki leikkaantuu, mutta niin tekee samalla voittomahdollisuutemme. Miksi? Koska todennäköisyys stop loss -toimeksiannon toteutumiselle kasvaa merkittävästi. Huomaa yllä olevasta VaR-laskelmasta, että mitä pienempi tappio-oletus sitä suurempi todennäköisyys on sen saavuttamiselle koska menemme lähemmäs tuottojen keskiarvoa.

Lataa artikkelin esimerkkipohja täältä.

Lue myös:

Sijoituksen tuoton laskeminen

Miten osakkeen hinta muodostuu?

Sijoittajan hyödylliset excel-kaavat

Sijoitustuottolaskuri