Keskeinen raja-arvolause

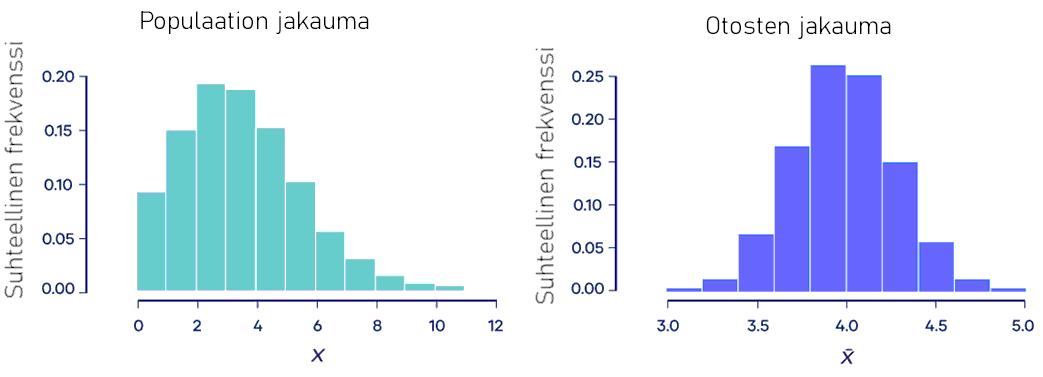
Keskeinen raja-arvo lause (Central Limit Theorem) on todennäköisyysteorian käsite, jonka mukaan otosten keskiarvojen jakauma vastaa likimain normaalijakaumaa otosten määrän kasvaessa, riippumatta populaation todellisesta jakaumasta mistä otokset ovat otettu.

Toisin ilmaisten, keskeinen raja-arvolause on tilastollinen lähtökohta, jonka mukaan otoksen koon ollessa riittävän suuri, kaikkien samasta populaatiosta otettujen muuttujien keskiarvo on suunnilleen yhtä suuri kuin koko populaation keskiarvo. Nämä otokset approksimoivat normaalijakaumaa, joiden varianssit (tai keskihajonnat) ovat suurin piirtein yhtä suuria kuin populaation varianssi otoksen koon kasvaessa suurten lukujen lain mukaisesti.

Otoskoon tulisi olla vähintään 30, että se on riittävä keskeisen raja-arvo lauseen kannalta. Kun otoskoko on riittävän suuri, voi sillä ennustaa populaation ominaisuuksia tarkemmin.

Keskeisen raja-arvolauseen tärkeimmät ominaisuudet:

• Otokset ovat peräkkäisiä, tarkoittaen että otos on yleinen edellisessä valitussa otoksessa.

• Valittujen otosten on oltava satunnaisia, jotta niillä on sama todennäköisyys tulla valituksi.

• Otosten tulisi olla itsenäisiä, eli niillä tai niiden pohjalta saaduilla tuloksilla ei tulisi olla vaikutusta tuleviin otoksiin tai niiden tuloksiin.

• Riittävän suuri otoskoko. Kun otoskoko kasvaa, lähenee otoksen jakauma normaalijakaumaa.

Käytännössä otoksia ei tarvitse toistuvasti ottaa populaation jakaumasta, jotta tiedettäisiin otosjakauma. Keskiarvoisen otosjakauman parametrit määrittelee populaatiojakauman parametrit.

• Otosjakauman keskiarvo on populaation keskiarvo. µ_x = µ

• Otosjakauman keskihajonta on populaation keskihajonta jaettuna otoskoon neliöjuurella σ_X̄ = σ / sqr(n)

• Otosjakauman keskiarvo X̄ ~ N(µ, σ / sqr (n))

Missä X̄ on otosjakauma otoskeskiarvoista, N on normaalijakauma, µ on populaation keskiarvo, σ on populaation keskihajonta ja n on otoskoko.

Keskeinen raja-arvolause rahoituksessa

Keskeinen raja-arvo lause on hyödyllinen rahoituksessa analysoitaessa yksittäisen arvopaperin tuottoja, tai laajempaa indeksiä, sillä sen mukaisen datan analysointi on varsin helppoa. Lauseen lautta voidaan arvioida salkun jakaumaa ja ominaisuuksia tuoton, riskin ja korrelaation suhteen.

Portfolioanalyysi: Oletetaan esimerkiksi, että jossakin pörssissä noteerataan, tai vaikka sijoittaja haluaa salkkuunsa 500 eri osaketta. Haluamme tutkia pörssin kokonaistuottoa. Tällöin voisimme poimia esimerkiksi ainakin 40–50 satunnaisesti valittua osaketta, (eri sektoreilta, kun poimitaan satunnaisesti) jotta keskeinen raja-arvo lause on voimassa ja voisimme arvioida koko pörssin tuottoa. Otospoiminta voidaan toistaa useasti, mutta aina edelliset otokset on poistettava puolueellisuuden (”bias”) poistamiseksi.

Tuottoanalyysi: Toisena esimerkkinä otetaan vain yksi osake, jolla pitkä tuottohistoria. Keskeisen raja-arvolauseen mukaan voisimme ottaa tuosta historiasta satunnaisia tuotto-otoksia eri aikajaksoilta, joilla voimme arvioida osakkeen koko populaation (koko historian) tuottokeskiarvon. Otoskeskiarvot tapaavat noudattaa normaalijakaumaa, mitä enemmän otosten määrä kasvaa.

Riskienhallinta: Kolmantena esimerkkinä sijoittaja voisi arvioida potentiaalisen sijoitussalkun tuottojakaumaa ja laskea jakaumasta ääriarvoja, kuten VaR-menetelmällä. Tämä onkin suosittu riskinhallintatapa, missä riskiä halutaan ottaa vain tietty määrä tietyllä luottamustasolla.

Keskeinen raja-arvolause on hyödyllinen analysoitaessa suuria tietojoukkoja, koska sen avulla voidaan olettaa, että keskiarvon näytteenottojakauma on useimmissa tapauksissa normaalijakautunut. Tämä mahdollistaa helpomman tilastollisen analyysin ja päätelmien tekemisen.