Normaalijakauma

Normaalijakaumaa sanotaan myös kellokäyräksi tai Gaussin käyräksi. Normaaliksi sitä sanotaan siksi, että 1800-luvulla lukuisissa tiedepapereissa useiden luonnonilmiöiden havaittiin tavallisesti tai "normaalisti" noudattavan Gaussin käyrää. Normaalijakauma on todennäköisyysjakauma ja tarkoittaa datan, eli useamman tapahtuman joukon tai havaintosarjojen jakautumista siten, että keskiarvo, mediaan ja moodi ovat samoja. Jakauma on myös symmetrinen, eli 50 % havainnoista on keskiarvon molemmin puolin.

Normaalijakauman oletus on tärkeä myös keskeisessä raja-arvolauseessa, jonka mukaan useiden otosten keskiarvot ovat normaalijakautuneita, riippumatta populaation jakaumasta. Oletus helpottaa tilastollista analyysiä ja päätelmien tekemistä.

Erilaisia jakaumia on useita, mutta normaalijakauma on yleisin ja sillä on esimerkiksi rahoituksessa useita erilaisia käyttökohteita, kuten teknisessä analyysissä tai omaisuuserien hinnoissa. Normaalijakauman muotoa noudattavat esimerkiksi ihmisten pituus, koetulokset, verenpaine tai rahoituksessa virhetermit ja tuottojen (logtuottojen) hajonta.

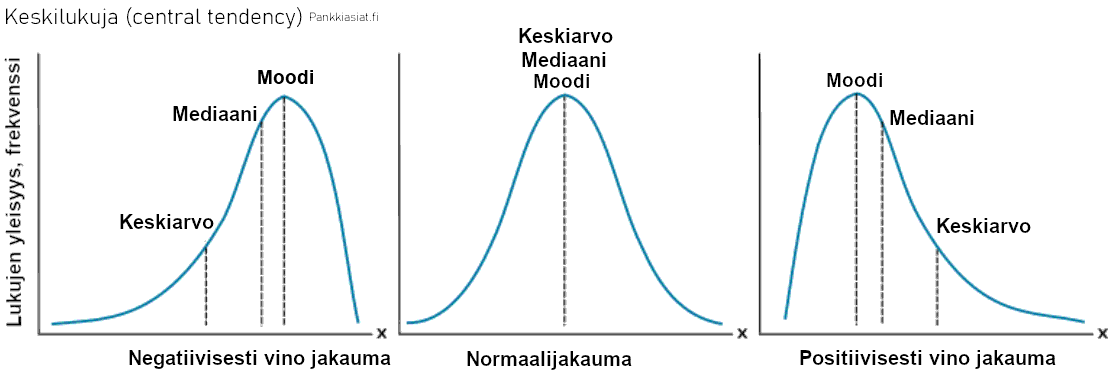
Normaalijakauman ominaisuudet

Normaalijakauman muoto voi vaihdella, mutta siten että se on silti symmetrinen. Kaikki symmetriset jakaumat eivät ole kuitenkaan normaalijakautuneita. Standardissa normaalijakaumassa on kaksi parametriä, keskiarvo ja keskihajonta.

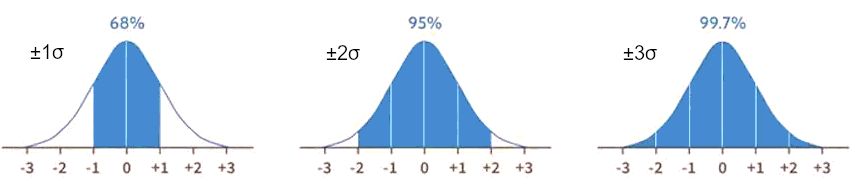
Niin sanotun empiirisen säännön mukaan normaalijakaumassa havainnoista 68,2 % tapahtuu plus tai miinus yhden keskihajonnan päässä keskiarvosta, 95,4 % kahden keskihajonnan ja 99,7 % kolmen keskihajonnan päässä. Yli kolmen keskihajonnan päähän sijoittuvat havainnot kuvaisivat erittäin harvinaista tapahtumaa, mitä usein käytetään osoittamaan "lähes varmaa" tapahtumaa, eli lähes varmasti kaikki tapahtumat ovat alle 3 keskihajonnan päässä.

Vinokkuus

Normaalijakaumassa vinokkuus (skewness) on nolla. Yllä olevassa 1. kuvasarjassa vasemmanpuolimmaisessa jakaumassa vinokkuus on negatiivinen, sillä sen vasen "häntä" on oikeaa pidempi. Vastaavasti oikeanpuolimmaisissa positiivinen ja pidempi häntä on oikealla.

Huipukkuus

Huipukkuus (kurtosis) tarkoittaa jakauman terävyyttä, tai tarkemmin se mittaa jakauman häntien paksuutta. Normaalijakauman huipukkuus on 0 tai standardisoidun normaalijakauman 3. Jos huipukkuus ylittää tämän arvon, jakauman sanotaan olevan terävähuippuinen (leptokurtic) tai jos alle, niin matalahuippuinen (platykurtic).

Normaalijakauma vs. standardi normaalijakauma

Normaalijakauman keskiarvo ja keskihajonta voivat olla periaatteessa mitä tahansa lukuja. Normaalijakauma voidaan standardisoida, jolloin puhutaan standardisoidusta normaalijakaumasta, jonka keskiarvo on aina 0 ja keskihajonta 1. Yllä 2. kuvasarjan esimerkissä jakaumat ovat standardisoituja, sillä keskiarvo on 0 ja keskihajonta perustuu standardilukuun Z.

Z = (Havainnoitava arvo - Keskiarvo) / Keskihajonta

Z-arvoa sanotaan standardipisteiksi, joka kertoo kuinka monen keskihajonnan päässä yksittäinen otoksen tai populaation arvo on keskiarvosta. Z-arvoja löytyy usein valmiiksi taulukoituina, mutta se on helppo saada myös esimerkiksi excel-funktiolla =NORM_JAKAUMA.KÄÄNT(todennäköisyys).

Katso tätä esimerkkiä tarkemmin lopun excel-tiedostosta. Vastaava tulos saadaan oli jakauma standardisoitu tai ei, eikä se ole tarpeellista aina. Standardisoimalla jakauman, voi siitä saada hyötyä seuraavissa käyttötarpeissa:

• Vertailla eri jakaumien pisteitä, joilla on erilaiset keskiarvot ja -hajonnat.
• Normalisoida pisteet tilastollisessa päätöksen teossa (esimerkiksi arvosanojen anto käyrältä)
• Löytää jakaumasta todennäköisyydet havainnoille jotka ovat yli tai ali annetun arvon
• Löytää todennäköisyyden että otoksen keskiarvo poikkeaisi merkittävästi populaation keskiarvosta

Standardisointi on helppoa, sillä se saadaan vähentämällä yksittäisestä arvosta otoksen keskiarvo ja jakamalla tulos otoksen keskihajonnalla.

Normaalijakauman laskenta

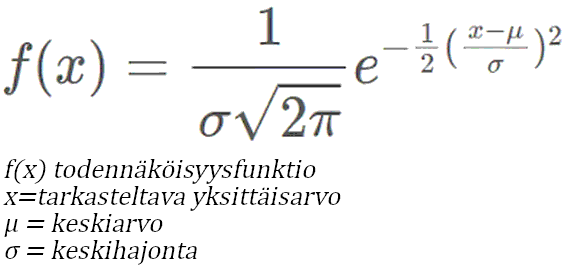
Jotta keskihajonta saadaan yksittäiselle arvolle, tarvitsee datajoukosta laskea vain keskiarvo ja keskihajonta. Taulukkolaskentaohjelmilla kuten excelissä normaalijakauman laskemiseen on valmiita funktioita:

• NORM_JAKAUMA.KÄÄNT, joka antaa käänteisen standardisoidun normaalijakauman kertymäfunktion, jonka keskiarvo on 0 ja keskihajonta 1.

• NORM_JAKAUMA.NORMIT, joka palauttaa standardisoidun normaalijakauman, jonka keskiarvo on 0 ja keskihajonta 1

• NORMAALI.JAKAUMA, joka palauttaa normaalijakauman itse määritetylle keskiarvolle ja -hajonnalle.

• NORMAALI.JAKAUMA.KÄÄNT, joka palauttaa käänteisen normaalijakauman kertymäfunktion itse määritetylle keskiarvolle- ja hajonnalle.

Alla on excel-tiedosto, jossa on valmiita normaalijakauman laskuesimerkkejä, sekä myös erilaisia testejä sille onko jokin jakauma normaalijakautunut, kuten Jarque-Bera, Q-Q plot ja myös tunnuslukujen analyysituloste.

Normaalijakaumaesimerkkejä.xlsx