Keskiarvo

Keskiarvo on arvojoukkoa edustava yksi luku. Aritmeettinen keskiarvo, eli tavallinen keskiarvo saadaan summaamalla arvojoukon luvut yhteen, jonka jälkeen ne jaetaan arvojen lukumäärällä. Keskiarvojen määritteitä on kuitenkin useita erilaisia, joita tarvitaan erilaisiin käyttötarkoituksiin.

Yleisimmät kolme keskiarvoa ovat aritmeettinen, geometrinen ja harmoninen keskiarvo, joita sanotaan myös pythagoralaisiksi keskiarvoiksi. Jos kaikki joukon arvot positiivisia, on geometrinen keskiarvo aina pienempi kuin aritmeettinen keskiarvo ja harmoninen keskiarvo aina pienempi kuin geometrinen keskiarvo. Jos kaikki arvot olisivat samoja, antaisi nämä keskiarvot saman tuloksen.

Erilaiset keskiarvojen laskentatavat huomioivat paremmin esimerkiksi arvojoukon poikkeavia arvoja, tai ominaisuuksia.

Aritmeettinen keskiarvo

Keskiarvo saadaan seuraavalla kaavalla:

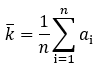
Kaavassa n on arvojen lukumäärä ja a on arvo, eli a arvot summataan ja jaetaan niiden lukumäärällä n. Esimerkiksi arvojoukon arvot ovat 5, 8, 12, 1, 9 ja niiden lukumäärä siten 5 kpl. Näin ollen:

Tästä saadaan myös muut keskiarvoon liittyvät käsitteet, kuten moodi ja mediaani. Moodi on yksinkertaisesti luku, joka esiintyy eniten arvojoukossa. Esimerkissä se on 6, koska se esiintyy kaksi kertaa ja muut vain kerran. Mediaani on taas keskimmäinen arvojoukon luku, eli esimerkissä 12.

Keskiarvo voidaan myös painottaa, eli saadaan painotettu keskiarvo. Silloin arvot kerrotaan niiden osuuksilla ja summataan, ja tulos jaetaan vielä painojen summalla. Esimerkiksi jos tuotto on 50 euroa 80 % todennäköisyydellä ja 100 euroa 20 % todennäköisyydellä, niin tuotto-odotus saataisiin painotettuna keskiarvona:

Painotettu keskiarvo on siten monissa tapauksissa tarkempi, kuin yksinkertainen keskiarvo. Se ottaa huomioon lukujen suhteellisen tärkeyden arvojoukossa.

Geometrinen keskiarvo

Geometrista keskiarvoa tarvitaan useimmin kun keskiarvoa lasketaan korreloituneista arvomuutoksista, tai kertoimellisista luvuista. Tällaisia ovat esimerkiksi sijoitusten tuottojen arvosarjat. Geometrinen keskiarvo huomioi tavallista keskiarvoa paremmin sijoitusten koronkoron vaikutuksen aikavälillä, varsinkin jos sijoituskohteen volatiliteetti on suuri.

Geometrinen keskiarvo saadaan kaavalla:

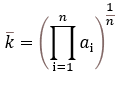
Esimerkiksi investoinnin tuotot ovat 5 %, 2 %, 1 %, 1 % 4 %, jolloin geometrinen keskiarvo tai sijoituksen keskiarvoinen tuotto:

Geometrisen keskiarvon korkoa korolle -vaikutuksen huomioiminen on sen ydin tuottoja laskiessa. Voikin sanoa, että aritmeettinen keskiarvo sopii yksinkertaiselle tuotolle, kun geometrinen keskiarvo sopii koronkoron huomioivalle tuotolle. Vastaava pätee myös muille arvosarjoille, joiden kertymät vaikuttavat seuraaviin prosenttiarvoihin. Geometrisen keskiarvon voi laskea vain positiivisille luvuille, kun aritmeettisen keskiarvon voi laskea myös negatiivisille.

Geometrista keskiarvoa voi sanoa myös oikaistuksi tuotoksi.

Harmoninen keskiarvo

Harmonista keskiarvoa käytetään erityisesti murtolukujen tai suhdelukujen keskiarvon laskentaan. Se on arvojen käänteislukujen aritmeettisen keskiarvon käänteisluku.

Harmoninen keskiarvo saadaan kaavalla:

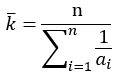
Esimerkiksi kolme tuottoa ovat 2 %, 4 %, ja 7 %, jolloin harmoninen keskiarvo on:

Joskus harmoninen keskiarvo on painotettava, jotta se antaa tasapainoisen tuloksen. Esimerkiksi yrityksen P/E suhdeluku on tällainen hintasuhdeluku, joka saadaan yritystasolla jakamalla yrityksen markkina-arvo sen nettotuloksella. Kolmen yrityksen P/E-luvut ovat 2, 4 ja 7 miljoonaa sekä niihin on sijoitettu 50 %, 30 % ja 20 % osuudet salkusta. joten painotettu harmoninen keskiarvo olisi:

Aritmeettisenä painotettuna keskiarvona tämä olisi 3,6 mikä olisi liikaa, joten harmoninen painotettu keskiarvo antaa tässä tapauksessa todellisemman kuvan sijoitussalkun keskimääräisestä P/E-luvusta.

Esimerkiksi Excelissä on valmiina KESKIARVO, KESKIARVO.GEOM ja KESKIARVO.HARM -funktiot keskiarvojen nopeaan laskentaan. Näitä funktioita ja lisää valmiita esimerkkejä on havainnollistettu keskiarvolaskurissa.