Korkoa korolle tai koronkorko (eng. compounding interest) tarkoittaa korkoa pääoman lisäksi kertyneille aiemmille koroille. Esimerkiksi pääomalle kertyy tuottoa, jolle voidaan edelleen ansaita tuottoa alkuperäisen pääoman lisäksi, eli pääoma kasvaa kiihtyvästi. Yksinkertaisella korolla pääoma kasvaa lineaarisesti.
Korkoa korolle laskenta
Koronkoron peruskaava:

Kaavassa n on laskennan aikajakson pituus korkojaksoina ja korkojaksot on vuoteen sisältyvien jaksojen määrä. Vuosikorko jaetaan korkojaksojen määrällä, eli saadaan jakson korkokanta.
Aikajakso lasketaan korkojakson mukaan, eli jos korkojakso on 1 päivä (eli korkojaksoja vuodessa 360) ja sijoitusaika 1,5 vuotta, olisi aikajakso 360 x 1,5 = 540 päivää. Tai jos korkojakso 1 kuukausi (korkojaksoja vuodessa 12), niin vastaavasti aikajakso 12 x 1,5 = 18 kuukautta.
Esimerkiksi jos vuosikorko on 5 %, korkojakso on 1 päivä, laskennan aikajakso n on 180 päivää ja pääoma 1000 €, niin tuotto-% tältä aikajaksolta olisi (kaava 1):
(1 + 5 % / 360)^180 -1 = 0,0253 eli 2,53 %.
Tuotto pääomalle (kaava 2) olisi 2,53 % x 1000 € = 25,3 €. Koronkorolla laskettua vuosituottoa voi sanoa myös todelliseksi vuosikoroksi, eli jos edellisen esimerkin (kaava 1) aikajakso n olisikin 360 päivää saksalaisen korkotavan mukaan, niin todelliseksi vuosikoroksi tulisi
(1 + 5 % / 360)^360 -1 = 0,0513 eli 5,13 %.
Esimerkiksi jos osakkeelle saadaan 10 % tuotto joka vuosi (korkojakso = 1), olisi alunperin 1000 € arvoisen sijoituksen arvo 5 vuoden päästä:
1,15 x 1000 = 1610,5 €, tai pidemmästi 1. vuonna 1000+1000 x 10 %= 1100 ja 2. vuonna 1100+1100 x 10 % = 1210 jne. ja 5. vuonna 1610,5 €.
(1+ korko)^n on vuosikorkotekijä, joka helpottaa laskuja sen sijaan että jokainen koronkoron erä laskettaisiin erikseen. Koronkorko voidaan laskea mille aikajaksolle tahansa, vaikka minuutille, jonka voisi laskea jatkuvan koron periaatteella.
Koronkorko vs. yksinkertainen korko
Pelkästään alkupääomalle yksinkertaisella korolla laskettu 10 % vuosituotto 5 vuoden aikajaksolla olisi tarkoittanut että sijoituksen arvo olisi 1500 € = (1+0,1 x 5) x 1000), eli toisin sanoen joka vuosi saisi 10 % tuoton 1000 eurolle, mutta ei kuitenkaan korkoa korolle. Korkoa korolle -osuus olisi näiden laskutapojen ero, eli 1610,5-1500 =110,5 €.
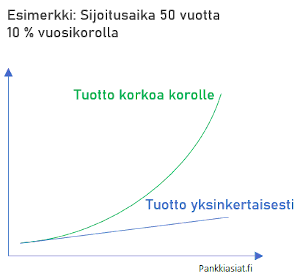 Korkoa korolle -vaikutus voimistuu sitä enemmän, mitä kauemmaksi mennään alkuhetkestä. Jos aikajaksoksi otetaan oheisen kuvan esimerkissä 50 vuotta, olisi korkoa korolle -summa kasvanut jo lähes 107 000 euroon. Yksinkertaisella tavalla summa olisi vain noin 6 000 €, joten ero on huima.
Korkoa korolle -vaikutus voimistuu sitä enemmän, mitä kauemmaksi mennään alkuhetkestä. Jos aikajaksoksi otetaan oheisen kuvan esimerkissä 50 vuotta, olisi korkoa korolle -summa kasvanut jo lähes 107 000 euroon. Yksinkertaisella tavalla summa olisi vain noin 6 000 €, joten ero on huima.
Yksinkertaisella koronlaskulla tuotto on aina sama alkupääomaan nähden, mutta koronkorolla joka vuosi kertyneet korot tai sijoitustuotot kerryttävät edelleen korkoa tai tuottoa.
Luottosopimuksissa koron periminen kertyneelle korolle on lailla kielletty, eli korko määräytyy jäljellä olevan tai alkuperäisen pääoman mukaan. Näin lasketaan myös joukkovelkakirjojen eli bondien tuotto.
Koronkoron valmiit funktiot
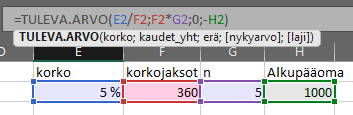
Koronkoron voi laskea helposti taulukkolaskentaohjelmilla kuten MS excel ja Google sheets. Esimerkiksi excel-ohjelmassa sen saa laskettua TULEVA-ARVO -funktiolla. Funktio käyttää juuri samoja muuttujia kuin kaavassa 2.
Funktiolla voi laskea nimensä mukaan esimerkiksi sijoituksen arvon n aikajakson päässä. Kaavassa korkokanta on 5 % / 360 = 0,014 %, joka on samalla päiväkorko. Aikajakso on 5 vuotta * 360 = 1800 päivää. Sijoituksen arvo olisi siten 5 vuoden päästä 1284 €.
Korkoa korolle laskelmia voi tehdä pankkiasiat.fi:n korkoa korolle laskurilla ta tuottolaskurilla.
Lisää korkoa korolle vaikutuksesta ym. laskuesimerkkeineen artikkelissa Tunnetko erilaiset korkokäsitteet?
