Jatkuva korko on koronlaskutapa, missä korko lasketaan aikavälin perusteella eksponentiaalisesti. Jatkuvassa korossa lasketaan korkoa korolle rajattoman monta kertaa. Jatkuvan koronlaskun tapa on olennainen rahoituslaskelmissa, mutta todellisuudessa se ei ole mahdollinen. Kun jatkuvan koron aikaväli pienenee äärettömän pieneksi, lähestyy korko valitun korkojakson suurinta korkoraja-arvoa.
Jatkuvan koron kaava:
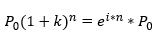
Kaava esittää koronkoron kaavan jatkuvan koron laskuna. Kaavassa P0 on alkupääoma, k on todellinen korko (1+korko/korkojaksot vuodessa)^korkojaksot vuodessa), i on korkointensiteetti ja n aikajakson pituus.
Lasketaan esimerkiksi 1000 eurolle 5 % vuosituotto jatkuvan koron perusteella vuoden päähän. Silloin summa olisi kasvanut vuodessa:
1000 x eksponentti (5 % x 1) = 1051,271096 euroon.
Jos edellinen olisi laskettu päiväkorkona koronkoron periaatteella, niin summa kasvaisi
1000 x (5 % / 365)365 = 1051,26750 euroon.
Lasketaan kasvu vain 50 päivälle. Silloin summa olisi kasvanut
1000 x eksponentti (5 % x 50 / 360) = 1006,968613 euroon.
Jos ensimmäisessä esimerkissä tuotto olisi laskettu yksinkertaisesti vuosikorkona yhdelle vuodelle, olisi tuotto yksinkertaisesti 1000 x 1,05 = 50 euroa. Mitä pienemmäksi laskentaperuste menee ja mitä enemmän kerrottuja aikavälejä, sitä lähemmäksi raja-arvoa valittu jaksokorko menee.
Jatkuvassa korossa eksponentti tarkoittaa neperin lukua, eli matemaattista vakiota 2,718 281 828 459... joka on luonnollisen logaritmifunktion kantaluku. Jatkuvassa korossa korkojakso on jaettava halutulla koronlaskuperusteella, joka on yleensä joko englantilainen vuosikorko tai saksalainen vuosikorko (esimerkissä käytettiin saksalaista vuosikorkoa, eli 50 jaettiin koronlaskuperusteella 360).
Jatkuva korko on tärkeä sijoitusten efektiivisen tuoton tai efektiivisen koron laskennassa.
