Beta

Beta tai beta-kerroin on sijoitusten arvonmäärityksessä käytetty riskikerroin. Se kertoo sijoituksen tuottojen herkkyydestä systemaattiselle riskille, eli markkinariskille. Beta-kertoimen vertailuarvo on 1, mikä tarkoittaa, että sijoituksen tuotto muuttuu keskimäärin samanarvoisesti markkinaportfolion tuottojen kanssa. Toisin sanoen jos kaikki markkinoilla olevat verrattavat sijoituskohteet olisivat samassa salkussa, muuttuisi sijoituksen tuotto samassa suhteessa tähän markkinaportfolioon.

Jos beta olisi alle 1, tarkoittaisi se että sijoituksen tuotot olisivat vähemmän herkkä markkinaportfolion tuottoihin vaikuttaville riskeille. Jos beta olisi yli 1, muuttuisi sijoituksen tuotto keskimäärin vastaavasti enemmän markkinaportfolioon verraten. Yleensä osakkeiden beta on välillä 0-3 ja esim. valtiovelkakirjoilla lähellä nollaa.

Negatiivinen beta on myös mahdollinen, mikä tarkoittaisi että sijoituksen tuotto muuttuisi vastakkaisesti markkinaportfolioon nähden. Negatiivinen beta on harvinainen, mutta joillakin johdannaisilla kuten myyntioptioilla beta voi olla negatiivinen. On myös joitakin osakkeita, jotka muuttuvat vastakkaisesti markkinasentimenttiin nähden.

Beta-kerroin on osa CAPM-mallin arvopaperin tuottovaatimuksen laskentaa. Beta kertoo markkinariskistä, jota ei voida hajauttaa pois. Se ei ole yksittäisen sijoituksen riskimittari kuten volatiliteetti, vaan riski suhteessa vertailuportfolioon.

Vertailuportfolio on yleensä arvopainotettu laaja osakeindeksi, mutta voi olla joku muukin; esimerkiksi kullan hintariskiä voisi verrata myös jalometalli-indeksiin.

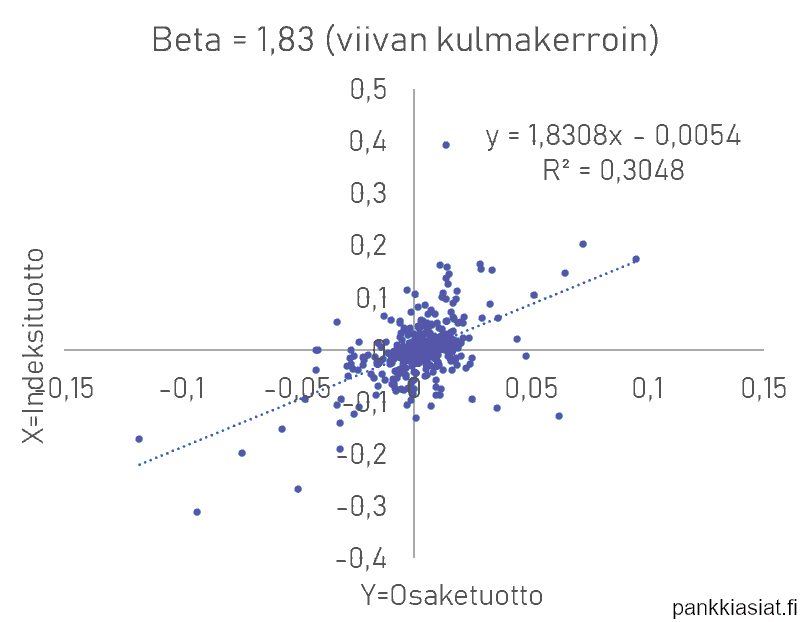
Esimerkkikuvassa on hajontakaavio vertailuindeksin ja osakkeen tuotoille. Beta on regressioviivan kulmakerroin. Selitysaste on matala ja beta korkea, mikä kertoo että osakkeen hinnassa on paljon vaihtelua, mitä vertailuindeksi ei selitä.

Miten beta lasketaan?

Beta on tilastollisesti laskettava luku, joka lasketaan sijoituskohteen ja vertailuindeksin historiallisten hintojen tuotoista ja niiden keskinäisen vaihtelun suhteesta. Betan laskemiseen on useampia tapoja.

1. Laskemiseen tarvitaan sijoituskohteen ja vertailuindeksin hintahistoria riittävän pitkältä jaksolta, esimerkiksi 3-5 vuotta. Aikasarjojen on oltava täsmääviä päivämääriltään.

2. Lasketaan aikasarjoista tuottosarjat yksinkertaisesti esim. Tuotto₂ = ( Hinta₂ / Hinta₁ ) -1

3. Lasketaan indeksin varianssi ja kovarianssi vertailuindeksin kanssa. Jaetaan sijoituskohteen ja vertailuindeksin kovarianssi sijoituksen varianssilla, tai vaihtehtoisesti suoritetaan tuottosarjoille lineaarinen regressio, jossa X = indeksi ja Y = sijoituskohde.

Beta-kertoimia on myös yleisesti saatavilla esim. arvopaperivälittäjiltä, joten itse laskeminen ei ole välttämätöntä. Betan voi laskea helposti esim. excel-ohjelmalla, jos osakkeen ja vertailuindeksin hintadataa on saatavilla. Valmis laskentamalli löytyy myös pankkiasiat.fi:n investointilaskurista. Excelin funktio KULMAKERROIN antaa betan suoraan.

Beta voidaan laskea eri aikaväleillä (päivä, kuukausi, vuosi) eri aikajaksoille, joten itse laskettuna saadaan arvo joka kuvaa parhaiten omaa käyttötarkoitusta.  Valitulla aikajaksolla on väliä esim. sen vuoksi, että sisältääkö laskettava väli jotain erityisiä tapahtumia jotka voivat vääristää laskentaa, kuten suuret hintapiikit ("outliers"). Itse laskettuna beta-kertoimen arvoon voi siten käyttää omaa harkintaa, mikä parantaa riskin tuntemusta.

Muita keskeisiä markkinoilla käytettäviä riskimittareita ovat volatiliteetti ja VaR (ja tähän perustuvat mittarit kuten taloudellinen pääoma). Katso myös alfa.