Varianssi

Varianssi on tilastollinen hajonnan mittari arvojoukon numeroiden välillä. Se mittaa miten kaukana numerot ovat koko joukon keskiarvosta eli muista numeroista. Varianssia merkitään yleensä symbolilla σ² , joka on kreikkalainen pieni kirjain sigma toiseen korotettuna.

Varianssia tarvitaan useissa sijoittamiseen liittyvissä konsepteissa, kuten esimerkiksi sijoituksen volatiliteetin määrittämisessä tai beetassa. Varianssin neliöjuuri on keskihajonta, eli volatiliteetti. Varianssia tarvitaan myös optimaalisen portfolion riski-tuottosuhteen laskennassa.

Varianssin laskenta

Varianssi lasketaan jokaisen numeron ja joukon keskiarvon erotuksena, jonka jälkeen erot korotetaan neliöön. Näin niistä tulee positiivisia arvoja eivätkä voi summautua nollaksi, mikä onkin yksi varianssin eduista. Lopulta arvot summataan yhteen ja jaetaan arvojoukon numeroiden määrällä.

Varianssin haittapuoli on mahdolliset suuret poikkeavuudet datassa, sillä jos nämä korottaa neliöön, niin ne voivat antaa datasta väärän kuvan koska näiden paino kasvaa liikaa.

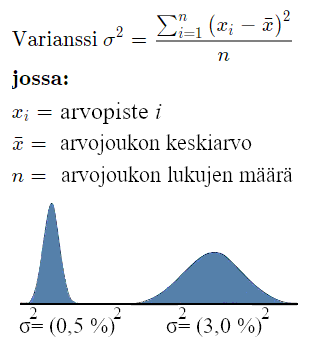
Suuri varianssi kertoo, että arvojoukon numerot ovat etäällä keskiarvosta ja pieni varianssi vastaavasti että ne ovat lähellä sitä. Jos varianssi olisi nolla, tarkoittaisi se että kaikki arvot olisivat identtisiä.

Osakkeen tuotot perättäisinä päivinä ovat  2 %, -5 % ja 6 %. Näiden keskiarvo on 1 %, joten tuottojen erot keskiarvosta ovat  1, -6 ja 5 (prosenttimäärät käsitellään kokonaislukuina). Edelleen neliöön korotettuna ja summaten saadaan 1^2 + -6^2 + 5^2 = 62 (eli 62 %).

Jaetaan 62 % vielä tuottojen määrällä, jolloin saadaan varianssi 62 / 3 = 20,67 eli 21 %. Jos tästä otetaan neliöjuuri, saadaan volatiliteetiksi 4,5 %.

Edellinen esimerkki koski populaation varianssin laskentaa. Toinen tapa on otosvarianssi, jossa n sijaan käytetään n-1 jakajana. Kun dataa on tarpeeksi suuri määrä, näillä ei ole käytännössä eroa. Otosvarianssi on nimensä mukaan otos suuremmasta joukosta, kun populaatiovarianssi käsittää koko joukon.

Esimerkiksi excelissä varianssin laskenta onnistuu helposti VAR.S ja VAR.P -funktioilla.

Portfolion varianssi

Portfolion varianssi on riskimittari ja se on painotettu yhdistelmä kovarianssin avulla säädettyjä yksittäisten sijoitusten variansseja.

Portfolion varianssin laskentaan tarvitaan kovarianssia tai korrelaatiokerrointa. Yleisesti ottaen jos portfolion sijoitukset korreloivat keskenään vain vähän tai negatiivisesti, niin myös portfolion varianssi on pieni. 

Portfoliovarianssin laskenta käy nopeasti hankalaksi ilman ohjelmaa, sillä mitä enemmän portfoliossa on sijoituksia, sitä nopeammin kaava kasvaa tarvittavien termien määrässä.

• w₁ = 1 sijoituksen paino
• w₂ = 2 sijoituksen paino
• σ₁= 1 sijoituksen keskihajonta
• σ₂ = 2 sijoituksen keskihajonta
• Kovarianssi_1,2 = 1 ja 2 sijoituksen kovarianssi eli p_(1,2)σ₁σ₂, missä p_(1,2) on sijoitusten korrelaatio