Ovatko esimerkiksi korkoa korolle, efektiivinen korko, nimelliskorko ja todellinen vuosikorko tuttuja käsitteitä? Miten ne liittyvät toisiinsa? Eri korkokäsitteet jakautuvat pääosin sekä koron ilmoitustapaan että laskutapaan, tai ne voivat myös olla molempia. Avaamme artikkelissa erilaisia korkokäsitteitä havainnollisten laskuesimerkkien kautta, menemättä liian syvälle korkomatematiikkaan.
Miksi koron tunteminen on tärkeää? Niin kauan kuin kuluttaja ei tunnista korkojen koukeroita, antaa se etua luotonantajille tai huonojen sijoitustuotteiden tarjoajille ja siten mahdollisuuden periä suuria kuluja. Suurin etu korkokäsitteiden tuntemisessa on siis parempien päätösten teko sijoituksissa ja laina-asioissa.
Koron erilaiset laskutavat
Vuosikorko
Vuosikorko on koron käsite yksinkertaisimmillaan, mutta aina hyvä tuoda esille alkupisteenä josta lähdetään laajentamaan koron tuntemista. Otamme artikkelissa esimerkiksi 1000 € pääoman ja 5 % vuosikoron. Siten jos 5 % vuosikorkoa maksetaan 1000 € alkupääomalle, olisi 1. vuoden tuotto 1000 € * 5 % = 50 € ja 2. vuoden tuotto 1000 € * 5 % = 50 eli yhteensä 100 € jne.
Sijoituksen vuosituottona pysyy näin sama 50 €. Tällainen yksinkertaisen koron tuote olisi joukkovelkakirja, mutta esimerkiksi osakkeessa vuosikorko kerryttää korkoa korolle joka on huomioitava kokonaistuotossa. Kuluttajalainoista kuten asuntolainoista puhuttaessa asiakas maksaa vuosikorkoa alenevalle pääomalle.
Vuosikorko voi sisältää erilaisia osia, esim. viitekoron ja marginaalikoron, tai se voi olla pelkästään kiinteä korko. Tyypillisimpiä ilmoitetun vuosikoron sovelluskohteita ovat erilaiset lainat, eli lainapääomasta (tai lainapääomalle) maksetaan vuosikorkoa. Vuosikorko voidaan pilkkoa pienempiin osiin, kuten kuukausikorkoon. Esimerkin 5 % vuosikorko olisi siten 5 % / 12kk = 0,42 % kuukausikorko. Korkojakso vaikuttaa vuosikoron tarkkaan määrään.
Korkoa korolle
Korkoa korolle, tai vanhahtavasti koronkorko, tarkoittaa tapaa laskea korkoa (tai tuottoa) myös korosta kertyvälle pääomalle. Eli jos 1. vuonna saataisiin 1000 € alkupääomalle 5 % korko, saamme 2. vuonna myös tälle 1. vuonna ansaitulle korolle korkoa. Eli 1. vuoden korko olisi 1000 € * 5% = 50 € ja 2. vuoden korko 1050 € * 5% = 52,5 € jne., jolloin 10. vuonna 1000 € alkupääoma olisi kasvanut 1628,9 euroon (vaihtoehtoisesti voidaan laskea 1000 € *(1+5%)^10 = 1628,9 €). Eli saadaan enemmän, kuin jos olisi ansaittu korkoa joka vuosi pelkästään alkupääomalle kuten yo. vuosikoron esimerkissä.
Korkoa korolle laskutapaa käytetään, kun lasketaan tuottoja talletuksille ja sijoituksille. Kun tuottoa on jo ansaittu, voidaan myös tälle ansaitulle tuotolle ansaita tuottoa. Usein sanotaankin, että nuoren sijoittajan paras ystävä on korkoa korolle -vaikutus, sillä mitä aiemmin sijoittamisen aloittaa, sitä enemmän tuottoa ehtii kertyä eläkeikään mennessä (ks. ao. kuva). Lain mukaan lainoista ei saa periä korkoa korolle -periaatteella, koska se voisi johtaa hallitsemattomaan velkaantumiseen.
Korkoa korolle laskuja voi tehdä lisää esim. pankkiasiat.fi:n korkoa korolle -laskurilla tai tuottolaskurilla.
Efektiivinen korko
Efektiivinen korko tai efektiivinen tuotto lasketaan jollekin halutulle aikajaksolle. Esim. jos yo. esimerkin mukaan 1000 € pääomalle saadaan 5 % vuosituottoa korkoa korolle 10 vuoden ajan, saataisiin 10 vuoden efektiiviseksi vuosituotoksi 6,29 %. Eli 1. vuoden tuotto 1000 € * 5% = 50 € ja 2. vuoden tuotto 1050 € * 5% = 52,5 € jne. ja 10. vuonna tuottoa olisi kertynyt 628,9 €. Siten efektiivinen tuotto 10 vuodelle olisi (628,9/1000 €)/10*100 = 6,29 %.
Kokonaistuotto 10 vuoden ajalta jaetaan alkupääomalla ja se edelleen 10 vuodella efektiivisen vuosituoton saamiseksi. Toisin sanoen, jos joka vuosi olisi saatu 6,29 % tuottoa 1000 € alkupääomalle (ei siis kertyvästi), olisi päästy samaan tulokseen.
Toinen esimerkki efektiivisestä korosta olisi sen laskeminen lyhyemmälle jaksolle kuin vuosi. Siten jos haluttaisiin laskea 1000 € alkupääomalle tuotto 3 kuukaudelle nimellisellä 5 % vuosituotolla ja joka maksettaisiin kuukausittain, saataisiin tuotto jakamalla 1 kuukausi 12 kuukaudella ja kertomalla se vuosikorolla, eli 1000 € * 5 % * 1/12 = 4,166 € tuotto 1. kuukautena. Toisena 1004,166 € * 5 % *1/12 = 4,184 € ja kolmantena 4,201 € eli yhteensä 12,551 €, joka on efektiivisesti 12,551 €/1000 € *100 =1,255 % kolmelle kuukaudelle.
Jos 5 % korko olisi 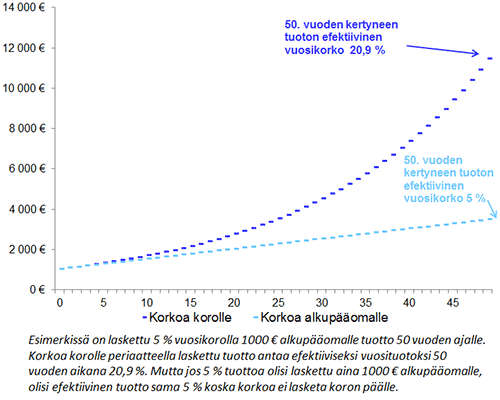 yksinkertaisesti jaettu 3 kuukaudelle eli 3/12 * 5 %, olisi tuotoksi saatu 1,250 % eli hyvin lähelle efektiivisesti laskettu tuottoa. Erot näkyvätkin yleensä sitä selvemmin mitä pidempi aikajakso on (koska tässä tapauksessa efektiivinen korko lasketaan korkoa korolle –tuotolle).
yksinkertaisesti jaettu 3 kuukaudelle eli 3/12 * 5 %, olisi tuotoksi saatu 1,250 % eli hyvin lähelle efektiivisesti laskettu tuottoa. Erot näkyvätkin yleensä sitä selvemmin mitä pidempi aikajakso on (koska tässä tapauksessa efektiivinen korko lasketaan korkoa korolle –tuotolle).
Efektiivisessä korossa voidaan laskea minkä tahansa aikajakson korko tai tuotto alkutilanteeseen nähden jakamalla tuotto vuosien määrällä (tai muu aikajakso jos halutaan jokin muu kuin vuosikorko). Efektiivistä korkoa käytetään myös lainmukaisen todellisen vuosikoron laskemisessa, jolloin siihen sisällytetään muitakin kuin korkokuluja.
Efektiivinen korko on periaatteessa tapa saattaa monimutkaisemmat tai vaihtelevat tuotot (ja mahdolliset kulut) vertailukelpoiseksi vuosikoroksi. Efektiivisen koron voi laskea useilla eri pankkiasiat.fi:n laskureilla.
Todellinen vuosikorko
Todelliseen vuosikorkoon voidaan lisätä muita kuluja koron lisäksi, kuten laskutuspalkkio. Esimerkiksi jos 1000 € lainasta maksetaan 5 % vuosikorkoa ja 10 € vuosittaista lainanhoitopalkkiota, olisi todellinen vuosikorko 6 %. Eli 10 € + 1000 € * 5 % = 60 €, joten 60 / 1000 * 100 = 6 %.
Todellinen vuosikorko tarkoittaa nimelliskoron lisäksi kaikki kulut huomioivaa korkoa jollekin aikajaksolle, yleisimmin vuoden ajaksi, jonka vuoksi yleisemmin puhutaankin lainmukaisesta todellisesta vuosikorosta esimerkiksi kuluttajalainojen osalta.
Todellinen vuosikorko on säännelty käsite, koska Euroopan talousalueella luotonantajien on ilmoitettava luoton todellinen kulut huomioiva vuosikorko tietyn kaavan mukaan. Tämä lasketaan ns. sisäisenä korkona.
Todellisen vuosikoron voi laskea esim. pankkiasiat.fi:n korkolaskurilla tai autolainalaskurilla.
Lue myös: Miten lainan korko lasketaan?
Koron ilmoitustapoja
Kuponkikorko
Kuponkikorko on velkakirjan arvolle maksettava ja emission yhteydessä ilmoitettu nimelliskorko, jonka mukaan kuponkimaksu määräytyy. Jos velkakirjan arvo muuttuu, muuttuu myös velkakirjan sijoitusajan tuotto, mutta kuponkimaksu pysyy samana.
Nimelliskorko
Nimelliskorko on periaatteessa mikä tahansa ilmoitettu korko, jossa inflaatiota tai muita reaalikorkoon vaikuttavia tekijöitä ei ole huomioitu. Esimerkiksi lainan 5 % vuosikorko, joka sisältää viitekoron ja margaalin, voi olla nimelliskorko. Nimelliskorko ei sisällä myöskään muita kuluja, vaan se on ilmoitettu peruskorko jollekin jaksolle; tavallisimmin yhdelle vuodelle.
Laskemalla nimelliskorkoa pääomalle ja tästä edelleen kertyvälle pääomalle, päästään korkoa korolle tuottoon. Tai jos lisätään nimelliskorkoon muita kuluja tai tuottoja, päästään todelliseen tai efektiiviseen korkoon. Nimelliskorosta voimme siis edetä koko ketjun efektiiviseen korkoon saakka. Kaikki muut ovat enemmän tai vähemmän näiden johdannaisia tai liitännäisiä.
Reaalikorko
Reaalikorko on perustasolla nimelliskorko vähennettynä inflaatiolla. Periaatteessa mikä tahansa korko tai tuotto voidaan esittää ”reaalisena” vähentämällä inflaation osuus, mutta yleisimmin sillä tarkoitetaan juuri nimelliskorosta vähennettyä inflaatiota. Reaalikorko on ennen kaikkea tapa suhteuttaa ansaittua tai maksettua korkoa aikaan, jonka kuluessa rahan arvo muuttuu.
Esimerkiksi jos 5 % nimelliskorkoa maksetaan pääomalle kertyvästi vuosittain 10 vuoden ajan, olisi yo. korkoa korolle esimerkin mukaan tuotto 1628,9 €. Mutta jos tästä 5 % nimelliskorosta vähennettäisiin 1 % inflaatio ja haluttaisiin tietää todellinen tuotto kun rahan arvon heikkeneminen huomioidaan (eli inflaatio), laskisimme saman esimerkin 4 % reaalikorolla ja saisimme loppusummaksi siten 1480,2 €. Voimme myös sanoa, että 1% inflaatiolla rahan arvosta on hävinnyt 10 vuoden aikana 1628,9-1480,2 € = 148,7 €. Reaalikorolla voi siis tarkentaa korkolaskelmia ja verrata tuottojen ostovoimaa eri aikajaksoina.
Reaalikorkoon ja tulevaisuuden tuottojen nykyarvoon liittyy keskeisesti diskonttaus.
Muita korkokäsitteitä
Viitekorko
Viitekorolla tarkoitetaan yleensä markkinakorkoa joka muuttuu rahapolitiikan mukaan, tai pankin omaa peruskorkoa joka muuttuu pankin päätöksen mukaan. Viitekorko on lainakorkojen muuttuva osa ja yleisesti puhutaankin, että "laina on sidottu" esim. euribor 12 kk viitekorkoon. Eli muutokset johtuvat yleisestä markkinakorosta.
Viivästyskorko
Viivästyskorkoa maksetaan luoton myöhässä olevalle erälle tai muulle laskulle. Viivästyskorko on kiinteä ja sen määrää rajoittaa laki, joka korvaa luotosta maksettavan koron viivästyksen veloitusajaksi.
Vaihtuva korko
Vaihtuva korko voi olla mikä tahansa korko, jossa on mukana muuttuva komponentti eli esim. markkinakorko kuten euribor. Siten esim. nimelliskorko, reaalikorko, vuosikorko jne. voi olla vaihtuvia. Myös todellinen vuosikorko ja efektiivinen korko voidaan laskea vaihtuvalle korolle.
Kiinteä korko
Kiinteä korko pysyy samana koko ajan ja onkin usein helpoin ymmärtää ja laskea. Kiinteä korko voi olla mikä tahansa korko, joka ei muutu.
Koroista lopuksi
Muitakin korkokäsitteitä esiintyy, mutta ne ovat yleensä aina samaa tai lähes samaa asiaa tarkoittavia käsitteitä eri nimellä. Jos jotain voidaan nostaa tärkeimmäksi aiheeksi muistaa tai ymmärtää yo. korkokäsitteistä, ovat nimelliskoron, koronkoron ja efektiivisen koron käsitteiden ja laskutapojen tunteminen. Nämä, näiden erot ja takana olevan idean tai matematiikan kun hallitsee, pärjää myös pitkälle lainakulujen ja sijoitustuottojen ymmärtämisessä.
Aiheeseen liittyvää:
Kiinteä korko, korkokatto vai vaihtuva korko?

![Tunnetko erilaiset korkokäsitteet [kuva]](https://pankkiasiat.fi/sites/default/files/styles/350x300/public/field/image/korkonopat.png)
![[Sijoittajan tärkeimmät tunnusluvut]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/investor.jpg)
![[Kuva] Yritysanalyysi: Kassavirtalaskelma](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/kassavirta_artikkelikuva.jpg)
![Yritysanalyysi:Tase [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/tase_artikkelikuva.jpg)


![Miten luottokortin korko lasketaan? [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/luottokortti_artikkelikuva.jpg)
![keskiarvo [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/keskiarvoartikkeli.jpg)
![[Reaalikorko ja sen vaikutus tuottoon]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/reaalikoro_artikkeli.jpg)
![Maksuohjelman laatiminen [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/lyhennysohjelma_artikkeli.png)
![Tuoton laskeminen [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/tuoton_laskeminen.jpg)
![Valuutanvaihtovertailu [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/valuutanvaihto_0.png)
![[voitokkaan sijoittajan 7 sääntöä]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/7-sijoittajan_saantoa.png)