Miten keskiarvo lasketaan?

Tavallinen keskiarvo, tai virallisemmin aritmeettinen keskiarvo on helppo laskea ja se onkin tuttu useimmille jo peruskoulusta. Keskiarvoja on kuitenkin useita erilaisia ja siten monia käyttötarkoituksia. Artikkelissa katsotaan tunnetuimpia keskiarvoja erityisesti rahoituksen näkökulmasta esimerkkien kera.

Tavallisen keskiarvon lisäksi mediaani, moodi, geometrinen- ja harmoninen keskiarvo sekä painotettu keskiarvo ovat kaikki keskiarvoja tai keskilukuja, jotka kuvaavat lukujoukon keskikohtaa. Vaikkapa mikä on yleisin, keskimmäisin, ehdot täyttävä tai tyypillisin keskiluku. Artikkelin lopusta pääsee lataamaan myös Excel- tai Google Sheets -pohjat, jossa on havainnollistettu keskiarvoja valmiilla esimerkeillä.

Aritmeettinen keskiarvo

Tämä on yleisin keskiarvo ja yksi pythagoralaisista keskiarvoista geometrisen ja harmonisen keskiarvon kanssa. Aritmeettisessa keskiarvossa luvut summataan yhteen ja jaetaan niiden määrällä. Esimerkiksi jos otetaan viisi satunnaista lukua väliltä 1-10, niin keskiarvo:

Jos sijoitus tuottaa kolmena edellisenä vuotena 5 %, -5 % ja 10 % tuotot, niin niistä saadaan esimerkkinä

Eli sijoituksen keskiarvoinen historiallinen vuosituotto on 6 %. Vertaa tätä geometriseen keskiarvoon alempana.

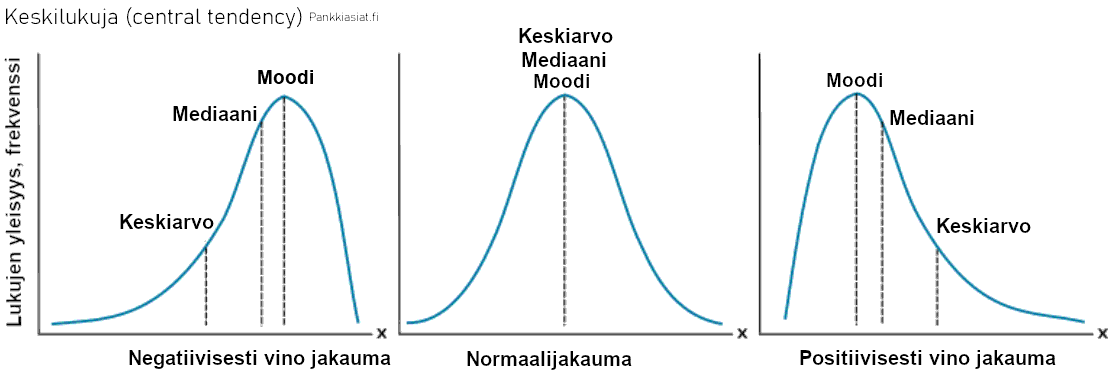
Mediaani

Mediaani on lukujoukon keskimmäisin luku. Mediaania laskettaessa luvut järjestetään pienimmästä suurimpaan, jolloin saadaan esimerkiksi:

Lukujoukon mediaani on 3 ja sen molemmille puolille jää kaksi lukua. Jos lukuja on pariton määrä, niin mediaani on suoraan keskimmäinen luku kuten yllä. Jos lukuja on parillinen määrä, esimerkiksi 1, 3, 3, 5, 7, 9, niin mediaani saadaan summaamalla kaksi keskimmäistä lukua yhteen ja jakamalla ne kahdella, eli kuten tavallinen keskiarvo:

Mediaani on aritmeettista keskiarvoa parempi kuvaamaan keskiarvoa, jos lukujoukossa on suuria poikkeamia, jotka vääristävät keskiarvoa.

Esimerkiksi jos lukujoukko on 1, 1, 2, 3, 10, niin aritmeettinen keskiarvo olisi 3, mutta mediaani 2. 2 olisi lukujoukkoa paremmin kuvaava keskiluku, koska arvo 10 on sen verran poikkeava muihin nähden.

Moodi

Moodi tarkoittaa lukujoukon yleisintä lukua. Mediaanin lukujoukon järjestelystä saadaan suoraan myös moodi. Eli lukujoukossa 1, 3, 3, 5, 9 yleisin luku on 3, sillä se esiintyy 2 kertaa kun muut esiintyvät vain kerran.

Jos joukkoon lisättäisiin vaikkapa 5, eli saadaan 1, 3, 3, 5, 5, 9, niin moodeja on nyt kaksi, eli ”moodisisarukset” 3 ja 5. Missä moodia tarvitaan? Moodi on vähiten käytetty keskiluku ja sitä tarvitaan useimmiten tilastotieteessä kuvaamaan joukon edustavinta lukua, tai kertomaan yleisimmät tapahtumat.

Painotettu keskiarvo

Painotettu on keskiarvosta erityistapaus, jossa jokaisen luvun tärkeys huomioidaan joukossa, eli luvun paino. Painotettu keskiarvo on hieman työläämpi laskettava kuin tavalliset keskiarvot, mutta ei silti vaikea. Otetaan jälleen viisi satunnaista lukua 2, 4, 1, 8, 9. Annetaan jokaiselle luvulle oma paino: 30 %, 20 %, 35 %, 10 %, 5 %.

Painotetussa keskiarvossa jokainen luku kerrotaan sen painolla ja parit summataan yhteen, sekä lopuksi jaetaan painojen summalla:

Jos painotuksia ei olisi tehty, olisi joukon tavallinen keskiarvo 4,8. Esimerkissä suuremmilla luvuilla on pienemmät painot, joten ne vaikuttavat vähemmän keskiarvoon.

Painojen tilalla voi käyttää myös todennäköisyyksiä. Esimerkiksi jos osakesalkun tuotto vuoden aikana on

10 % todennäköisyydellä 0 %,

30 % todennäköisyydellä 5 %,

50 % todennäköisyydellä 10 % ja

10 % todennäköisyydellä 15 %,

niin saamme osakesalkulle laskettua odotetun tuoton:

Odotettu tuotto on tärkeä käsite monissa rahoituksellisissa laskennoissa. Erityinen esimerkki painotetusta keskiarvosta on WACC, eli painotetusta pääoman kustannuksesta, joka on tärkeä esimerkiksi yrityksen arvonmäärityksessä tai diskonttauksessa.

Geometrinen keskiarvo

Geometrinen keskiarvo kuvaa keskiarvoa logaritmisella asteikolla. Sitä käytetään, kun keskiarvoa tarvitsee laskea eri yksiköille, tai lähinnä kasvua kuvaaville kuten kilometri, litra, korkeus, tuotto jne. Geometrista keskiarvoa ei voi laskea negatiivisista tai nolla-arvoista.

Rahoituksessa geometrinen keskiarvo on hyödyllinen korkoa korolle -vuosituoton laskennassa, tai efektiivisessä vuosituotossa johon se sopii aritmeettista keskiarvoa paremmin. Tuottojen vaikutus muutetaan kertoimiksi 1 + tuotto. Esimerkiksi sijoituksen tuotot kolmena vuonna ovat 5 %, -5 % ja 15 %. Tuottojen geometrinen keskiarvo on:

Eli tuottojen määrät n kpl kerrotaan keskenään ja niistä otetaan n:s juuri (tai korotetaan 1/n potenssiin). Geometrinen keskiarvo antaa tässä tapauksessa osakesalkun keskimääräisen vuosittaisen kasvuvauhdin. Sillä voi muuntaa eri mittaisten aikajaksojen tuotot vertailukelpoiseksi korkoa korolle -vuosituotoksi (CAGR), mikä helpottaa eri sijoitusten vertailua.

Nyrkkisääntönä voisi sanoa, että kun lukuja kerrotaan, käytetään geometrista keskiarvoa ja kun niitä lisätään, käytetään aritmeettista keskiarvoa.

Harmoninen keskiarvo

Harmonista keskiarvoa käytetään keskiarvon laskemiseen kahden eri yksikön suhdeluvusta, kuten nopeus, kiihtyvyys, korko tai erilaiset suhdeluvut ja kertoimet. Nimellisesti se tarkoittaa lukujoukon käänteislukujen keskiarvon käänteislukua. Myöskään harmonista keskiarvoa ei voi laskea negatiivisista tai nolla-arvoista.

Harmonista keskiarvoa voisi käyttää esimerkiksi yrityksen tunnusluvuille, kuten P/E, P/B, jne. Näin voisi laskea esimerkiksi yrityksen keskimääräisen tehokkuuden valituilla tunnusluvuilla.

Otetaan kolme eri mittaista sijoitusta, joilla voi ansaita 5 % 1 vuoden sijoituksella, 10 % 2 vuoden ja 15 % 3 vuoden sijoituksella. Sijoitusten keskimääräinen harmoninen pitoaika olisi:

Harmonista keskiarvoa voi siis käyttää keskiarvon laskentaan, jossa lukuja voidaan ilmoittaa suhdelukuina tai käänteislukuina.

Muita keskiarvoja

Erilaisia keskiarvoja on kymmeniä, joten emme käy kaikkia läpi. Joillakin keskiarvoilla on hyvin erityinen käyttötarkoitus, johon se sopii paremmin kuin muut. Tunnettuja muita keskiarvoja tai käsitteitä:

Generalisoitu tai yleistetty keskiarvo, joka kattaa koko joukon erilaisia keskiarvoja, kuten yllä laajemmin käsitellyt ns. pythagoralaiset keskiarvot (aritmeettinen, geometrinen, harmoninen).

Neliöllinen keskiarvo, jota käytetään lähinnä insinööritieteissä kuten sähkötekniikassa. Sitä voi pitää myös yleistetyn keskiarvon erityistapauksena.

Winsoroitu keskiarvo, jossa lukujoukon tietty osuus suurimmista tai pienimmistä arvoista korvataan pienimmillä ja/tai suurimmilla ääriarvoilla. Idea on rajoittaa ääriarvojen osuutta lukujoukossa. Kun halutut arvot on korvattu, voidaan keskiarvo laskea aritmeettisesti.

Trimmattu keskiarvo lasketaan kuten winsoroitu keskiarvo, mutta siinä ääriarvot jäävät kokonaan pois. Esimerkiksi jos lukujoukon molemmista päistä leikataan 10 % arvoista, niin näitä ei korvata ääriarvoilla. Muuten trimmauksen jälkeen lasketaan kuten aritmeettinen keskiarvo.

Jos lukujoukot ovat muutamia kymmeniä arvoja suurempia, kuten satoja, tuhansia tai jopa miljoonia, niin erityisissä keskiarvoissa lukuja ei enää useimmiten poimita tai muokata käsin, vaan ohjelmallisesti käytetään sopivaa jakaumaoletusta, kuten normaalijakauma ja tästä leikataan tietty osa arvoista, tietyillä oletuksilla.

Tällaisia ovat esimerkiksi kvartiili- tai kvantiilikeskiarvot, eli nimensä mukaan trimmaus tai winsorointi rajoitetaan tiettyihin jakauman osiin, vaikkapa neljänneksiin tai kymmenyksiin, tai mihin tahansa osaan. Vieläpä useissa erilaisissa lukujen jakaumissa.

Näin ollen keskiarvoja voidaan laskea lähes rajattomasti erilaisilla tavoilla, vaikka edelleen yleisin ns. ”arkikäytössä” on se tuttu aritmeettinen keskiarvo, millä pärjää pitkälle. Mutta joissain tilanteessa on parempi korvata se tarkoitukseen sopivalla keskiarvolla.

Pääset lataamaan keskiarvoesimerkkien laskentapohjan lisähavainnollistuksineen täältä.

Lue myös:

Sijoituksen tuoton laskeminen