Lainan korko ilmoitetaan yleensä vuosikorkona ja se määräytyy markkinakoron sekä lainanmyöntäjän marginaalin perusteella. Korko voidaan jakaa tästä edelleen kuukausille tai päiville, mutta jos korkoja halutaan laskea tulevaisuuteen tai jollekin aikajaksolle, vaikuttaa korkolaskelmiin moni asia. Käymme tässä artikkelissa perustasolla läpi lainakorkoja ja kuinka lainan lyhennystapa vaikuttaa maksettuihin korkoihin aikajaksolla.
Artikkelin lopusta löytyy korkolaskuri, sekä myös laskuri tasaerälainan, annuiteettilainan ja tasalyhennyslainan (ja hieman eksoottisempien bullet- ja balloon-lainojen) vertailuun.
Lainan vuosikorko
Olkoon esimerkkilainassa markkinakorkona 12 kuukauden euribor, joka on lainakoron muuttuva osuus eli viitekorko. Asetetaan markkinakoroksi 0,1 % laskentahetkellä, minkä lisäksi huomioidaan marginaali eli pankin kiinteä korko-osuus, jonka suuruus riippuu asiakkaasta. Olkoon marginaali esimerkissä 1,0 %.
Lainan vuosikorko on laskentahetkellä siten yhteensä 1,1 %, kun edellä mainitut lainakoron osat lasketaan yhteen. Kuukausikoroksi muutettuna tämä olisi 1,1 % / 12 = 0,0917 %, tai päiväkorkona 1,1 % / 365 = 0,003 % mikä on tarkempi lainakoron laskutapa. Näin kuukausikorko 1,1 % * 30 / 365 = 0,0904 %. Kuukausikorko kertoo, paljonko lainan kuukausierän korko-osuus olisi.
Kuukausikorko voitaisiin muuttaa myös takaisin vuosikoroksi (1 + 0,0917 %) ^12 - 1 = 1,106 %, mistä tulee hiukan alkuperäistä vuosikorkoa suurempi korkoa korolle vaikutuksen vuoksi. Päiväkorko olisi vastaavasti (1 + 0,003 %) ^365 - 1= 1,106%, mikä antaa pyöreästi saman tuloksen vuosikoroksi. Jatkuvalla korkolaskulla saataisiin vieläkin tarkempi, raja-arvoa lähestyvä tulos mutta tätä tapaa ei lainalaskuissa käytetä.
Korko lasketaan useimmiten päiväkorkoperusteisesti pidemmille aikajaksoille todellisten päivien mukaan, joita normaalivuonna on 365 tai karkausvuonna 366.
Jos korkokuluihin lisättäisiin avauspalkkiot, laskutuspalkkio ym. sivukulut, saataisiin todellinen vuosikorko.
Korkolasku lainasaldon ja ajan mukaan
Jos esimerkkilainan määrä olisi 100 000 euroa, olisi korkojen määrä 100 000 *1,1 % = 1100 euroa vuodessa, tai 100 000 * 0,0917 % = 91,7 euroa kuukaudessa ja 100 000 * 0,003 % = 3,0 euroa päivässä. Mutta lainan saldon alentuminen on huomioitava, mikä vaatii maksutaulun luontia.
Koron voisi laskea päiväperusteisesti mille tahansa aikajaksolle, vaikka kuluttajalainoissa tämä onkin harvinaista muulle kuin kuukaudelle. Esimerkiksi viivästyskorko on tällainen. Korko 50 päivän ajalle laskettaisiin (50 / 365 * 1,1 %) * 100 000 = 150,7 euroa. Laskettaessa korkoa vuotta pienemmille aikajaksoille, voi pientä eroa syntyä riippuen vuosikoron laskutavasta. Suomessa käytetään nykyisin englantilaista vuosikoron laskutapaa.
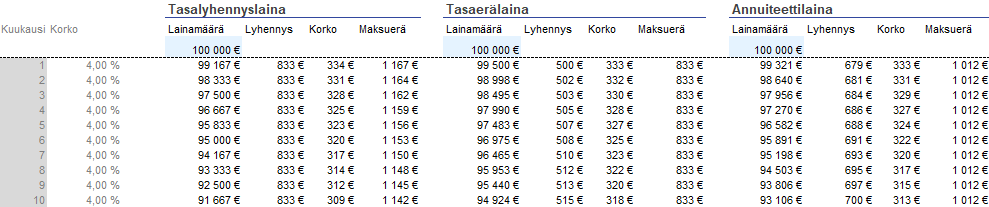
Kun lainaa lyhennetään, pienenee myös lainapääoma ja sille maksettava korko. Oletetaan, että yllä olevaa 100 000 € lainaa lyhennetään 500 euroa kuukaudessa, mistä tulee 6000 euroa vuodessa. Siten lainapääomaa olisi vuoden jälkeen jäljellä 94 000 euroa.
Paljonko olisi korkoja maksettu lainasta tämän mukaan, sen sijaan että laskettaisiin koko lainasummalle vuosikorko 1100 euroa?
Helpointa on rakentaa vaikkapa excel-ohjelmalla maksutaulu, mutta havainnollistamme periaatteen myös lyhyesti tässä. Lainan korko lasketaan joka kuukausi alenevalle pääomalle. Ensimmäisen kuukauden korkomaksu on yllä mainittu 91,7 euroa, mutta toisen kuukauden korkomaksu lyhennyksen jälkeen on 99 500 * 1,1 % / 12 = 91,2 euroa ja kolmannen 99 000 * 1,1 % / 12 = 90,8 euroa jne.
Koko vuoden korkomaksuiksi tulee 1100 euron sijasta 1069,8 euroa, koska lainaa on lyhennetty. Tarkemmin vuodessa maksettavat lainan korko- tai lyhennysmäärät riippuvat onko kyseessä tasaerälaina, annuiteettilaina vai tasalyhennyslaina.
Jos oletetaan, että markkinakorko pysyisi samana, helpottuvat korkolaskut ja maksuerä pysyisi samana laina-ajan tasaerä- ja annuiteettilainoissa. Todellisuudessa korot muuttuvat ennen pitkää koronmääräytysmisjakson päätteeksi, kuitenkin vain kerran vuodessa jos valittu viitekorko on vaikkapa 12 kk euribor.
Lainakorkolaskelmia maksuohjelmineen voi tehdä valmiilla pankkiasiat.fi korkolaskurilla tai lainalaskurilla. Erilaisten lyhennystapojen eriä voi vertailla kätevästi vierekkäin lyhennystapalaskurilla, jossa on myös havainnollisia kuvia erilaisten lyhennystapojen korko- ja pääomien suuruudesta laina-ajalla.
Tasalyhennyslainan koron laskeminen:
Koska lyhennysosa on koko laina-ajan sama tasalyhennyslainassa, vähentää se lainapääomaa aina saman määrän. Esimerkiksi 100 000 - 500 = 99 500 - 500 = 90 000 - 500 jne. jos lyhennys on 500 euroa.
Korko-osa on muuttuva ja lasketaan aina jäljellä olevan lainapääoman mukaan, esimerkiksi 100 000 * 1,1 % / 12 = 91,7 ja 99 500... = 91,2 jne. Koko maksuerä olisi 1. kuukautena siis 500 + 91,7 = 591,7 euroa ja 2. kuukautena 591,2 euroa jne. Jos korko nousee, nousee maksettava korko mutta lyhennys ei muutu.
Katso tarkemmin kuinka tasalyhennyslainan korko lasketaan.
Tasaerälainan koron laskeminen:
Tasaerälainan maksuerä, eli korko + lyhennys on laina-ajan yhtä suuri. Jos korko nousee, lyhenee laina hitaammin koska koron osuus maksuerästä nousee. Silloin laina-aika pitenee ja korkokulut kasvavat huomattavasti. Oletetaan, että maksuerä olisi 600 euroa ja 1. lainakuukauden korkoerä edelleen 91,7 euroa. Lyhennyksen osuus on 600 - 91,7 = 508,3 euroa ja lainamäärä siten 99 491,7 euroa.
Jos kuvitteellisesti korko nousisi heti 2. kuukautena 2,2 % tasolle, olisi seuraava korkomaksu 99 491,7 * 2,2 % / 12 = 182,1 euroa, jolloin toinen lyhennysosa olisi 600 - 182,1 = 417,9 euroa. Todellisuudessa esimerkiksi 12 kk euriboriin sidotun lainan korko voi nousta vasta 12 kk jälkeen.
Jos tasaerälainan korko nousee erityisen paljon, jopa lähes maksuerän kokoiseksi, ei laina lyhene vaan maksuerää on tällöin nostettava tai maksettava loppu laina kerralla pois. Pankeilla on monesti ehto, että tasaerälaina muuttuu annuiteettilainaksi, jos tasaerälainan maksuaika venyisi erittäin pitkäksi (yli 25-30 vuotta).
Katso tarkemmin kuinka tasaerälainan korko lasketaan.
Annuiteettilainan koron laskeminen:
Annuiteettilaina on tasaerälainan kaltainen (tasaerälainan laskutapa on myös annuiteetti), mutta laina-aika ei muutu koron noustessa (ei ylitä, mutta voi olla hiukan lyhyempi). Korko nousee koronmääräytymisjakson jälkeen, jolloin maksuerää nostetaan vastaamaan loppua laina-aikaa jotta laina saadaan lyhennettyä määräajassa.
Katso tarkemmin kuinka annuiteettilainan korko lasketaan.
Korkomaksujen lasku käsin on työlästä, joten on parempi ottaa avuksi laskentaohjelma, kuten excel. Olemme tehneet lyhennystapalaskurissa eri lainatyypeille valmiit maksuohjelmakaavat, jolloin vain laina-aika, vuosikorko ja lainamäärä tarvitsee syöttää ja vertailu on helppoa. Laskurissa on mukana myös havainnollisia automaattisesti päivittyviä kuvia eri lyhennystavoista, kun lainatietoja muutetaan. Nopeisiin ja tarkempiin lainakululaskelmiin sopii korkolaskuri.
Excel-ohjelmassa ja monissa muissa taulukkolaskentaohjelmissa on useita valmiita komentoja, joilla lainalaskuja voi tehdä nopeasti. Näitä on käyty läpi artikkelissa hyödylliset excel-kaavat korkolaskuille.
Katso myös:
Muut Pankkiasiat.fi laskurit

![Lainakoron laskeminen [kuva]](https://pankkiasiat.fi/sites/default/files/styles/350x300/public/field/image/korkonoppa.jpg)
![[Sijoittajan tärkeimmät tunnusluvut]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/investor.jpg)
![[Kuva] Yritysanalyysi: Kassavirtalaskelma](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/kassavirta_artikkelikuva.jpg)
![Yritysanalyysi:Tase [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/tase_artikkelikuva.jpg)


![Miten luottokortin korko lasketaan? [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/luottokortti_artikkelikuva.jpg)
![keskiarvo [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/keskiarvoartikkeli.jpg)
![[Reaalikorko ja sen vaikutus tuottoon]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/reaalikoro_artikkeli.jpg)
![Maksuohjelman laatiminen [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/lyhennysohjelma_artikkeli.png)
![Tuoton laskeminen [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/tuoton_laskeminen.jpg)
![Valuutanvaihtovertailu [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/valuutanvaihto_0.png)
![[voitokkaan sijoittajan 7 sääntöä]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/7-sijoittajan_saantoa.png)