Raha-asiointiin kuten lainoihin, sijoittamiseen, säästämiseen ja henkilökohtaiseen taloudenpitoon liittyy monenlaista laskentaa. Excel on oivallinen apu, jolla erilaiset laskut onnistuvat nopeasti, kunhan keskeiset kaavat tunnetaan. Katsotaan artikkelissa muutamia käteviä kaavoja korkoprosenttien ja maksuerien laskentaan.
Oletamme, että käyttäjällä on perustuntemusta excelistä ja laskutaidoista. Jos ei ole, niin ei se mitään, selitämme kaavoja esimerkkien kera. Käytämme exceliä, mutta muitakin vastaavia hyviä taulukkolaskentaohjelmia on, kuten ilmainen LibreOfficen Calc, joissa on useimmat vastaavat komennot kuin excelissä.
Kokosimme excel-tiedostoon valmiiksi yleisimpiä korkolaskuihin liittyviä komentoja, joita tarvitaan raha-asioiden hoitamisessa tai sijoittamisessa. Muutamia näistä käydään läpi seuraavana.
Otetaan kaavojen pohjalle esimerkki, jossa laina-aika (tai sijoitusaika) on 10 vuotta, vuosikorko on 5 % (tai vuosituotto) ja maksuerä (tai tuottoerä) on 100 € vuosittain. Kaavoilla voi tehdä yhtä hyvin sijoitusten tuottolaskuja kuin lainalaskuja.
Käytetään yksinkertaisuuden vuoksi vuotta perusaikajaksona. Jos aikajaksona olisi esimerkiksi kuukausi, niin kaavoissa korko tulisi jakaa 12:sta ja 10 vuotta tulisi kertoa 12 maksuerien saamiseksi.
Korkolaskujen kaavat
KORKO -funktio palauttaa korkokannan kausittaiselle annuiteetille, eli säännölliselle maksuerien sarjalle kuten lainanhoidon erille, sisältäen lyhennyksen ja koron.
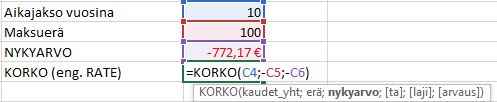
Funktiossa on syötettävä kausien määrä, eli esimerkiksi 10 vuotta, jos maksuväli on vuosittainen. Erä on maksuerän koko, esimerkiksi 100 €. Nykyarvo on alkusijoituksen tai lainan määrä, jolle saadaan säännöllisiä tuottoeriä tai se voi olla vaihtoehtoisesti laina, jota maksetaan takaisin.
Nykyarvon ja maksuerän on oltava kaavassa negatiivinen luku, mikä noudattaa excelin logiikkaa. Erää ei ole pakko syöttää, mutta silloin tarvitaan tuleva arvo, johon sijoituksen oletetaan kasvavan.
Kuvan esimerkin voi ajatella niin, että 772 € sijoitukselle saadaan vuosittain 100 € tuottoa 10 vuoden ajan. KORKO palauttaa sijoituksen vuosikoron, eli tässä tapauksessa 5 %. Jos tällä korolla diskontattaisiin maksuerät koko ajalta, palauduttaisiin nykyarvoon.
KORKO.EFEKT -funktio palauttaa todellisen vuosikoron jos korkojakso on muu kuin vuosi. Esimerkiksi jos 5 % nimellinen vuosikorko lasketaan kuukausittain, on tämä komento yhtä kuin (1 + 5 % / 12) ^12 = 5,12 %. Tässä kannattaa huomata, että yleensä todellisesta vuosikorosta puhuttaessa tarkoitetaan kaikkien lainakulujen huomioivaa korkoa, joka on eri asia. Tästä excelin kaavasta olisi oikeastaan parempi puhua korkojaksojen mukaisena vuosikorkona.
SISÄINEN.KORKO -funktio laskee sisäisen korkokannan säännölliselle rahavirtasarjalle. Näiden rahavirtojen ei tarvitse olla tasasuuruisia, kuten annuiteetissa. Näiden on kuitenkin oltava säännöllisiä, kuten kuukausittain tapahtuvia.

Kuvassa rahavirtojen sisäinen korko olisi 13 %. Sisäinen korko on sama laskentatapa kuin Euroopan kuluttajasuojalain mukainen todellinen vuosikorko. Todellisen vuosikoron laskentaa voi kokeilla lisää valmiilla korkolaskurilla.
SISÄINEN.KORKO.JAKSOTON -funktio on muuten sama kuin SISÄINEN.KORKO, mutta tässä rahavirtojen ei tarvitse olla säännöllisiä. Ne voivat olla epäsuuruisia epäsäännöllisin väliajoin.

Sisäinen korko liittyy läheisesti nettonykyarvon laskentaan. Sisäinen korko on korko, jolla nettonykyarvo on 0. Vastaavasti excelissä jaksoton sisäinen korko on vastaava jolla jaksoton nettonykyarvo on 0 kun päivämäärät ja erät ovat samoja.
MSISÄINEN -funktio palauttaa sisäisen korkokannan, kun alkusijoituksen ja tästä saatavien uudelleensijoitettavien rahavirtojen korkotuotot ovat erilaisia. Taustalla on oletus, ettei mennyttä tuottoa voida välttämättä sijoittaa enää eteenpäin samalla menneellä tuotto-oletuksella.
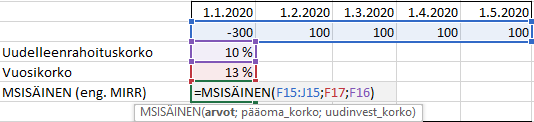
Esimerkiksi jos alkuperäisen sijoituksen tuottojen sisäinen korkokanta on 13 % ja tuotot sijoitetaan uudelleen 10 % tuotto-odotuksella, niin MSISÄINEN antaa näiden kahden sijoituksen ja niiden tuottojen yhdistetyn sisäisen korkokannan. Esimerkissä tämä tulos on 12 %.
Maksu- ja korkoerien kaavat
Artikkelissa lainan maksusuunnitelman laatiminen on valmis MAKSU, PPMT ja IPMT -funktioita käyttävä lainan lyhennyssuunnitelma excel tai sheets versioina.
MAKSETTU.KORKO -funktio laskee kertyneen koron haluttujen jaksojen väliltä laina-aikana (tai sijoitusaikana).
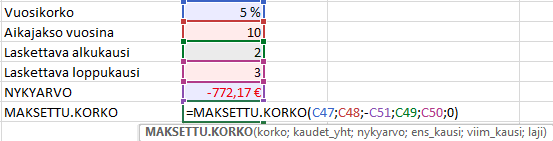
Esimerkiksi jos lasketaan 10 vuoden sijoituksen korko vuosien 2 ja 3 väliltä, saadaan kertyneeksi koroksi 67,9 €. Huomaa, että tämä sisältää molemmat vuodet 2 ja 3. Jos korko halutaan yhdeltä vuodelta, niin ensi- ja loppukausi asetetaan samaksi. Kaava antaa silloin saman tuloksen kuin IPMT.
MAKSU- funktio laskee maksuerän annuiteettilainalle tai sijoitukselle, joka perustuu säännöllisiin maksueriin ja kiinteään korkoon.

Esimerkin tulokseksi tulee 100 €, joka on sama erä jolla olisimme laskeneet KORKO-funktion vuosikoron 5 %. Excelissä löytyykin oma kaava tuntemattoman muuttujan löytämiseen, kun ainakin kaksi muuta muuttujaa tunnetaan. Tässä yhteydessä nämä ovat MAKSU, NA ja KORKO.
IPMT -funktio palauttaa säännöllisiin maksueriin ja kiinteään korkoon perustuvan lainan (tai sijoituksen) tietyn kauden korkoerän.
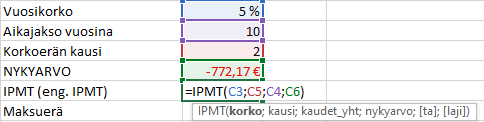
Esimerkissä korkoerä laskettaisiin 2. vuodelta, jolloin se olisi 35,5 €
PPMT -funktio on muuten sama kuin IPMT, mutta se palauttaa säännöllisiin maksueriin ja kiinteään korkoon perustuvan lainan (tai sijoituksen) tietyn kauden lyhennyserän.
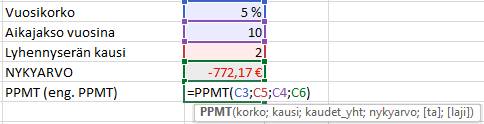
Esimerkissä lyhennyserä laskettaisiin 2. vuodelta, jolloin se olisi 64,5 €.
Esimerkeissä esiintyneet kaavat löytyvät tarvittaessa tästä excel-pohjasta.
Lue myös:


![[Sijoittajan tärkeimmät tunnusluvut]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/investor.jpg)
![[Kuva] Yritysanalyysi: Kassavirtalaskelma](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/kassavirta_artikkelikuva.jpg)
![Yritysanalyysi:Tase [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/tase_artikkelikuva.jpg)


![Miten luottokortin korko lasketaan? [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/luottokortti_artikkelikuva.jpg)
![keskiarvo [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/keskiarvoartikkeli.jpg)
![[Reaalikorko ja sen vaikutus tuottoon]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/reaalikoro_artikkeli.jpg)
![Maksuohjelman laatiminen [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/lyhennysohjelma_artikkeli.png)
![Tuoton laskeminen [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/tuoton_laskeminen.jpg)
![Valuutanvaihtovertailu [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/valuutanvaihto_0.png)
![[voitokkaan sijoittajan 7 sääntöä]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/7-sijoittajan_saantoa.png)