Prosenttilaskennan osaaminen tärkeää lähes kaiken aikaa, koskipa se tuotteiden hintamuutoksia, korkoprosenttia, sijoitustuottoja tai muiden eri lukujen vertailuja. Perusmuotoinen prosenttilasku on selvää useimmille, mutta osa on sellaisia laskuja, joista kokeneempikin joutuu hiukan miettimään että ”miten tämä menikään...” vaikka kouluaikoina nämä ehkä osattiinkin. Vaikeatkin prosenttilaskut ovat lopulta varsin yksinkertaisia, kun ne puretaan osiin. Lähdetään muistin virkistykseksi liikkeelle perusasioista, siirtyen lopussa esimerkkien kautta hiukan vaativampaan prosenttien pyörittelyyn.
Prosenttikäsitteet
Prosentti tarkoittaa perusmuodossaan sadasosaa kokonaisesta luvusta 100, mitä käytetään vakiintuneena tarkkuutena suhteellisten osuuksien tai muutosten ilmaisemiseen. Sana tulee latinasta Pro Centum = yksi sataa kohti (1/100). Muita tarkkuuksia olisivat Pro Decem = yksi kymmentä kohti (1/10), tai Pro Mille, yksi tuhatta kohti (1/1000).
Symboli ” % ” on vakiintunut prosentin lyhyt ilmoittamiskäytäntö, mutta yhtä hyvin prosentin voi ilmoittaa perusmuodossaan sadasosina 1/100, tai desimaaleina 0,01 mikä helpottaa laskentaa. Prosentti saadaan kertomalla desimaali sadalla.
Prosenttiosuus tarkoittaa osuutta kokonaisesta, eli prosentin tapauksessa sadasta. Jos vihreitä omenoita on 20 kpl ja punaisia 80 kpl, olisi omenoita kaikkiaan 100 kpl. Voidaan siis sanoa, että vihreiden omenoiden määrä on 20 sataa omenaa kohti, eli 20/100 joka on desimaalina 0,2. Desimaali on aina kerrottava sadalla jotta saadaan prosentti, eli 0,2 * 100 = 20 %. Jos punaisia omenoita olisikin 60 kpl, sanottaisiin että vihreitä omenoita on 20 kpl 80 omenaa kohti. Siten 20/80 = 0,25, jolloin vihreitä omenoita on 0,25 * 100 = 25 % eli 25 kpl sataa omenaa kohden.
Prosenttimäärä tarkoittaa prosenttiluvun mukaista yksikkömäärää. Esim. 20 % vastaava kappalemäärä ylläolevan ensimmäisen esimerkin mukaan on 20 kpl vihreitä omenoita, eli prosenttimäärä on siis 20 kpl. Jälkimmäisessä esimerkissä prosenttimäärä on 25 kpl, kun todellinen määrä on 20 kpl vihreitä omenoita.
Prosenttimuutos on jonkin määrän positiivinen tai negatiivinen muutos. Esimerkiksi vihreitä omenoita syödään 5 kpl, jolloin jäljelle 15 kpl. Vihreiden omenoiden muutos voidaan ajatella osuutena, eli laskenta menisi samoin kuin prosenttiosuuden kohdalla jolloin syötyjä omenoita olisi 5/20 eli 25 % vihreistä omenoista on syöty. Täsmällisemmin omenoiden muutos ilmoitetaan -5 kpl, eli -5/20 * 100 = -25 %, eli tämän verran vihreiden omenoiden määrä on muuttunut. Jos puheesta käy ilmi muutoksen suunta, ei etumerkkiä välttämättä tarvitse. Mutta pelkkä -25 % kertoisi muutoksen suunnan.
Prosenttiyksikkö tarkoittaa prosenttiosuuksien välisiä (absoluuttisia, ei suhteellisia) eroja tai etäisyyksiä. Esimerkiksi 1 % ja 5 % välinen ero on 4 % prosenttiyksikköä. Voidaan esim. sanoa, että korko nousi 4 prosenttiyksikköä, mutta olisi väärin sanoa, että korko nousi 4 prosenttia. Jos korko nousisi 4 prosenttia, olisi muutos prosenttiyksikköinä 4 sadasosaa (4/100, tai 0,04), eli uusi korko olisi 1,04 %. (1 + 0,04).
Prosenttipiste on usein ammattimaisesti käytetty laskutapa, kun laskettavat muutokset ovat pieniä ja vaativat tarkkuutta. Esimerkiksi rahoitusmarkkinoilla puhutaan usein korkopisteistä laskettaessa lainan hintoja tai tuottoja, mikä on prosentin sadasosa, eli tavallaan sadasosan sadasosa. Yksi korkopiste (”one basis point”) = 0,01 % eli desimaalina 0,0001.
Prosenttilaskuja voi tehdä kätevästi myös excel-prosenttilaskurilla
Prosentin laskeminen osuuksina ja muutoksina
Prosentin laskemisessa tärkeää on perusarvo eli alkuperäinen luku, mistä prosenttia lähdetään laskemaan. Tähän verraten prosenttiosuudet tai -muutokset on helpompaa laskea. Laskettavista osista kannattaa siis muodostaa ensin kokonaissumma perusarvoksi, joka on 100 %. Prosenttilaskua voi vielä helpottaa ajattelemalla osuudet tosielämän tilanteessa, jos valmista laskutilannetta ei ole jo saatavana. Olkoon esimerkkinä rahamääräinen omaisuus 150 €, josta 60 € on tilillä ja 90 € osakkeessa. Muunnetaan nämä prosenttiosuuksiksi:
Tilillä on 60 € / 150 € = 0,4, eli 0,4 * 100 = 40 % (tai 40 sadasosaa) omaisuudesta on turvallisena talletuksena.
Osakkeena on 90 € / 150 € = 0,6, eli 0,6 * 100 = 60 % omaisuudesta on alttiina sijoitusriskille.
 Koska tilistä ja osakkeesta tulee yhteensä 150 €, on tämä 100 % omaisuudesta eli perusarvo. Jos osakkeita olisikin esim. kaksi tai haluttaisiin laskea vain sijoituksen hintamuutos, otettaisiin perusarvoksi 90 €.
Koska tilistä ja osakkeesta tulee yhteensä 150 €, on tämä 100 % omaisuudesta eli perusarvo. Jos osakkeita olisikin esim. kaksi tai haluttaisiin laskea vain sijoituksen hintamuutos, otettaisiin perusarvoksi 90 €.
Osakesijoituksen arvo laskee 50 euroon, mikä on 55,6 % alkuperäisen sijoituksen 90 € perusarvosta (50 € / 90 € = 0,556, jolloin 0,556 * 100 = 55,6% eli jäljellä oleva prosenttiosuus alkuperäisestä sijoituksesta). Siten arvo on laskenut 44,4 % koska 100 %- 55,6 % = 44,4 %. Vaihtoehtoisesti voidaan laskea arvonmuutoksen osuus suoraan -40 € / 90 € *100 = -44,4 %, mikä on prosenttimuutos alkuperäiseen sijoitukseen nähden.
Haluamme laskea koko omaisuuden arvonmuutoksen, joten perusarvoksi on otettava alkuperäinen 150 €. Silloin osakkeen 40 € arvonlasku on laskenut omaisuuden arvoa 110 euroon, jolloin jäljellä on 110 € / 150 € *100 = 73,3 % omaisuudesta. Muutos olisi -40 € / 150 € *100 = -26,7 % eli tämän verran omaisuus on menettänyt arvoaan. Jos kokonaissumma muodostuu osista, kuten tässä tilitalletuksesta ja sijoituksesta, niin prosenttiosuudet tai -muutokset voidaan laskea sekä osille että kokonaissummalle. Perusarvoksi otetaan summa johon muutokset tai osuudet halutaan verrata.
Prosenttilaskussa muutokset ja osuudet on helpointa laskea jakamalla ne perusarvolla. Jos itse perusarvo on laskettava, saadaan se jakamalla osuus prosenttiluvulla.
Ei ole väliä otetaanko tililtä rahaa vai muuttuuko sijoituksen arvo, sillä muutos lasketaan samalla tavalla ja eri muutoksia voi myös summata. Esimerkissä talletuksen ja sijoituksen osuudet koko omaisuudesta kuitenkin muuttuvat.
Jos yo. esimerkissä omaisuuden uusi arvo olisi 110 €, olisi talletuksen osuus 60 € / 110 € * 100 = 54,5 % ja sijoituksen 50 € / 100 € * 100 = 45,5 % koko omaisuudesta. Talletuksen rahamääräinen arvo olisi edelleen sama, mutta sijoituksen taas ei. Toisaalta talletuksen suhteellinen arvo koko omaisuuteen nähden kasvaa, kun taas sijoituksen arvo laskee.
Jos sijoituksen arvo nousisi em. laskun jälkeen 70 €, olisi uusi kokonaisarvo 50 € + 70 € = 120 € ja koko omaisuus siten 120 € + 60 € = 180 €. Sijoituksen arvo olisi noussut 70 € / 50 € * 100 = 140 %. Jos arvonnousua sen sijaan verrattaisiin alkuperäiseen sijoitukseen 90 €, olisi arvo noussut ”vain” 33,3 % (30 € / 90 € * 100 = 33,3 %.
Koko omaisuuden arvo olisi noussut 30 € / 150 € = 20 %, eli 1,0 + 0,2 = 1,2, jolloin 1,2 * 150 = 180 €. Jos jatkossa vertaamme uusia muutoksia uuteen arvoon, esim. sijoituksen 120 € tai omaisuuden 180 € arvoon, niin tämä uusi arvo on silloin otettava perusarvoksi.
Peräkkäiset prosenttimuutokset
Jos vertaamme arvonmuutoksia vain perusarvon ja lopullisen arvon kesken, sanotaan tätä efektiiviseksi prosenttimuutokseksi eli pituuden mukaiseksi tai todelliseksi muutokseksi. Silloin perusarvon ja lopullisen arvon (tai vertailuarvon) välissä on voinut tapahtua mitä tahansa arvoon vaikuttava, eli esim. yo. sijoituksen arvon lasku ennen sen nousua lopulliseen arvoonsa. Siten esim. perusarvo ja lopullinen arvo voidaan saada useina peräkkäisinä arvonmuutoksina.
Sijoituksen arvo on alussa 100 €, mutta laskee sitten 10 %, nousee taas 20 %, laskee 5 %, nousee 5 % ja nousee vielä 10 %. Aina edellisen arvonmuutoksen jälkeen saamme uuden perusarvon, johon uusi arvonmuutos lasketaan: Alkumuutos 100 € * -10 % = -10 €, joten 100 € - 10 € = 90 €, josta seuraava muutos 90 € * 20 % = 18 €, eli 90 € + 18 € = 108 € jne. mutta tämä on melko työläs laskutapa.
Laskenta helpottuu, kun kerrotaan täyteen arvoon (100 %) lisättyjen tai vähennettyjen muutosten jälkeiset arvot suoraan keskenään. Siten 90 % * 120 % * 95 % *105 % * 110 % = 118,5 %, eli sijoituksen arvo on kasvanut 118,5 euroon kaikkien muutosten tuloksena (desimaalikertoimena 1,185 * 100 €). Tuotto on siis efektiivisesti 18,5 %. Tällainen laskutapa tunnetaan myös korkoa korolle -laskuna, eli käytännössä näin lasketaan myös sijoitustuotot tai muut peräkkäiset hintamuutokset.
 Prosentin ominaisuuksiin kuuluu, että positiivinen prosenttimuutos voi olla äärettömän suuri, mutta negatiivinen muutos voi olla korkeintaan 100 %. Esimerkiksi sijoitus kasvaa 100 eurosta 500 euroon, jolloin tuottoprosentti olisi 400 %. Tämän jälkeen sijoituksen arvo laskee nollaan, jolloin muutos on -100 %.
Prosentin ominaisuuksiin kuuluu, että positiivinen prosenttimuutos voi olla äärettömän suuri, mutta negatiivinen muutos voi olla korkeintaan 100 %. Esimerkiksi sijoitus kasvaa 100 eurosta 500 euroon, jolloin tuottoprosentti olisi 400 %. Tämän jälkeen sijoituksen arvo laskee nollaan, jolloin muutos on -100 %.
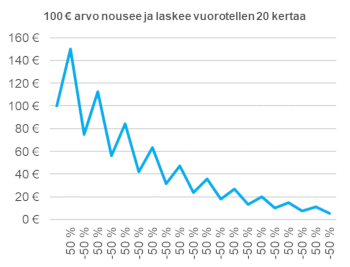
Samansuuruinen negatiivinen ja positiivinen prosenttimuutos ovat kerrannaisvaikutukseltaan erisuuruisia. Havainnollistetaan esimerkillä: Miten käy kun 100 € arvon nousee ja laskee 50 % vuorotellen 20 kertaa? Sijoituksen arvo olisi lopussa vain 5,6 € eikä suinkaan 100 €, mikä näkyy myös oheisessa kuvassa.
Jos edelliset peräkkäiset prosenttimuutokset laskettaisiin aina alkuperäiselle perusarvolle 100 €, voitaisiin ne laskea suoraan yhteen: -10 % + 20 % - 5 % + 5 % + 10 % = 20 %, eli alkuperäinen 100 € kasvaisi 120 euroon (1,2 * 100 €). Esimerkiksi lainakorot on laskettava alkuperäiselle tai lyhentyvälle saldolle, eikä maksettavalle korolle saa enää maksaa uutta korkoa. Lisää koronlaskuperiaatteista artikkeleissa Tunnetko erilaiset korkokäsitteet ja Miten lainan korko lasketaan.
Useita prosenttiosuuksia ja prosenttimuutoksia voidaan summata ja kertoa kuin mitä tahansa lukua, riippuen siitä mikä on asetettu perusarvoksi eli mitä halutaan selvittää. Tämä nopeuttaa laskemista.
Prosenttilasku päässä ilman laskinta
Vaativammatkin prosenttilaskut ovat lopulta melko yksinkertaisia, kun omaksuu prosentin perusominaisuuden yksi sataa kohti. Miten lasketaan esim. 4 % summa 860 eurosta? Lasketaan ensin 1 %, eli jaetaan 860 sadalla jolloin saadaan 8,6. Tämä kerrotaan neljällä, jolloin saadaan vastaus. Jos desimaalien laskeminen päässä on hankalaa, voidaan desimaalitkin pilkkoa vielä osiin. Lasketaan ensin kokonaisluku, eli desimaalin vasen puoli 8 * 4 = 32, pidetään se muistissa ja lasketaan vielä 4 * 6 = 24. Koska desimaalissa on tässä esimerkissä kyse kymmenyksistä, pitää se jakaa vielä kymmenellä eli saadaan 2,4. Siten 4 % on 32 + 2,4 = 34,4 €. Paljonko on 80 % 860 eurosta? 10 % on 86 €, joka voidaan kertoa kahdella eli saadaan 172 €, joten 860 - 172 € = 688 €.
Lopulta prosenttilaskussa on kyse melko yksinkertaisesta kerto-, vähennys- ja yhteenlaskusta, mutta myös jonkin verran muistia vaaditaan. Desimaaleja laskettaessa jaetaan tulos jaetaan halutun tarkkuuden mukaan, esim. 0,68 laskettaisiin (6*4)/10 + (8*4)/100 mutta yleensä arkipäiväisissä tilanteissa yhden desimaalin, tai pelkän kokonaisluvun tarkkuuskin riittää. Jokainen voi luoda itselle laskentaa helpottavia yksinkertaisia muistisääntöjä, eikä yhtä oikeaa tapaa ole. Paljonko on esim. 5,5 % alennus 860 eurosta? Lasketaan ensin 1 % kuten yllä ja kerrotaan viidellä, eli saadaan 43 €. Prosentin desimaali saadaan helposti; lasketaan samoin kuin koko prosentti mutta jakamalla kymmenellä, eli saadaan 4,3 €. Siten 5,5 % on 43 + 4,3 = 47,3 €. Hiukan harjoittelemalla laskut alkavat sujua nopeasti.
Lisää laskuesimerkkejä
Laskuesimerkeissä prosentit ovat ilmoitettu desimaalimuodossa.
- Alkuperäinen hinta (perusarvo)
Osakkeen hinta laskee 10 %, jolloin uusi hinta on 20 €. Alkuperäinen hinta on 20 / (1,0-0,1) = 22,2 €.
- Pienentyvä prosenttiosuus perusarvosta
Rahaa on 1000 €, josta 60 % on säästöjä, josta 50 % talletuksia, josta edelleen 30 % tilitalletuksia, josta 20 % säästötilillä. Koko omaisuudesta säästötilillä on 1000 € * 0,6 * 0,5 * 0,3 * 0,2 = 18 €. Jokaisen rahamäärän osuus saadaan samalla tavalla.
- Suurentuva prosenttiosuus perusarvosta
Säästötilillä on 18 €, joka on 20 % tilitalletuksista, tilitalletukset 30 % kaikista talletuksista, talletukset 50 % säästöistä ja säästöt 60 % kokonaisvaroista. Kokonaisvaroja on siten 18 € / 0,2 /0,3 / 0,5 / 0,6 = 1000 €.
- Useat samanaikaiset arvonmuutokset
Tilillä on 50 € ja osakkeessa 100 €, yhteensä 150 €. Tililtä otetaan 20 € ja osakkeen hinta nousee 10 €. Kokonaisarvonmuutos: Nosto laskee tilin arvoa 40 % (20/50), jonka osuus arvonmuutoksesta 50/150 * -0,4 = -0,133. Sijoituksen arvo nousee 10 % (110/100), jonka osuus arvonmuutoksesta 100/150 *0,1 = 0,067. Siten -0,133+0,067=-0,067, eli arvonlasku kaikkiaan -6,7 % arvoon 140 €. Samaan toki pääsee laskemalla arvonmuutokset yhteen ja lisäämällä ne perusarvoon 150 € (joten 140/150 = 0,067 neg. muutos).
- Sama korkoprosentti ansaitaan useita kertoja
Pääomalle 100 € ansaitaan 5 % joka vuosi 10 vuoden ajan. Siten lopullinen rahamäärä on 100 € * 1,05^10 = 163 € jos myös vuosittain kertyneelle pääomalle maksetaan tuottoa. Jos 5 % maksetaan vain alkupääomalle aina uudestaan, on lopullinen rahamäärä 100 € + 0,05 * 10 * 100 = 150 €. Laskutapojen ero on korkoa korolle -vaikutus.
Muuta aiheeseen liittyvää:

![Miten lasketaan prosentti ? [kuva]](https://pankkiasiat.fi/sites/default/files/styles/350x300/public/field/image/prosenttilasku.png)
![[Sijoittajan tärkeimmät tunnusluvut]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/investor.jpg)
![[Kuva] Yritysanalyysi: Kassavirtalaskelma](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/kassavirta_artikkelikuva.jpg)
![Yritysanalyysi:Tase [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/tase_artikkelikuva.jpg)


![Miten luottokortin korko lasketaan? [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/luottokortti_artikkelikuva.jpg)
![keskiarvo [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/keskiarvoartikkeli.jpg)
![[Reaalikorko ja sen vaikutus tuottoon]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/reaalikoro_artikkeli.jpg)
![Maksuohjelman laatiminen [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/lyhennysohjelma_artikkeli.png)
![Tuoton laskeminen [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/tuoton_laskeminen.jpg)
![Valuutanvaihtovertailu [kuva]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/valuutanvaihto_0.png)
![[voitokkaan sijoittajan 7 sääntöä]](https://pankkiasiat.fi/sites/default/files/styles/tiny/public/field/image/7-sijoittajan_saantoa.png)