Optimaalinen sijoitussalkku

Millainen on optimaalinen sijoitusportfolio, eli ”salkku” ja kuinka se optimoidaan? Optimaalinen sijoitussalkku on sellainen, jossa haetaan suurinta tuottoa pienimmällä riskillä ja niiden yhdistelmillä. Laskemme artikkelissa useista Helsingin pörssin yhtiöstä riski-tuottosuhteen ja etsimme tehokkaasta rintamasta optimaalisen sijoitussalkun.

Käytetään laskennassa excel-ohjelmaa. Valittsimme yhtiöt tähän esimerkkiin varsin sattumanvaraisesti, mutta ne ovat kuitenkin tunnetummasta päästä. Laskentaan tarvitaan osakkeiden hintadataa, jota löytyy esimerkiksi Yahoo finance -sivuilta. Yhtiöitä on valittu laajahko salkku, yhteensä 17 kpl ja jokaiselle hintahistoria 1 vuoden ajalta.

Datan valinnassa kannattaa huomioida, millaisia tapahtumia se sisältää. Esimerkiksi vuosi 2020 oli monille osakkeille hyvin poikkeuksellinen niiden historiaan nähden, joka voi vaikeuttaa tulkintaa. Jätämme tämän artikkelin esimerkissä huomioimatta.

Nopeasti voi vaikuttaa siltä, että salkun optimoinnissa on liikaa työtä. Mutta kun malli on kerran luotu, niin jatkossa optimointi sujuu nopeasti. Löydät myös artikkelissa käytetyn mallin artikkelin lopusta.

Osakkeiden riskiluvut

Hintahistorian perusteella lasketaan jokaiselle sarjalle tuotot kaavalla ( Hinta t1 / Hinta t-1 ) -1, eli nykyinen hinta jaetaan edellisellä hinnalla miinus 1.

Kun tuotot on laskettu, laskemme saaduista tuottosarjoista, keskiarvoisen tuoton, varianssin ja keskihajonnan. Näiden laskenta on helppoa excelin KESKIARVO, VAR.S ja KESKIHAJONTA -funktioilla. Jos datan hintaväli on alle vuosi, niin nämä kannattaa muuntaa vuosiarvoiksi tulkinnan ja käyttökelpoisuuden vuoksi.

Esimerksi jos väli on päivä, niin varianssi ja volatiliteetti voidaan skaalata ylöspäin funktiolla =Volatiliteetti*NELIÖJUURI (252). Tämä siksi, koska kaupankäyntipäiviä on noin 252 vuodessa.

Saamme näiden vaiheiden jälkeen osakkeille ja niiden riskiluvuille seuraavanlaisen taulukon:

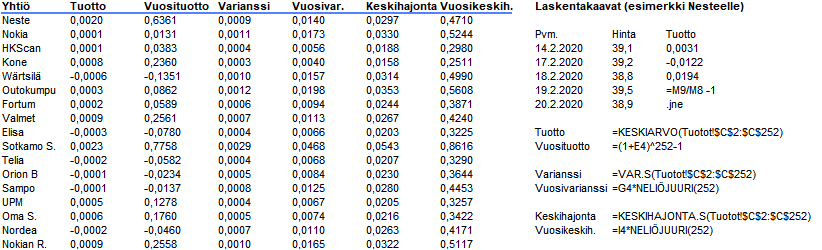
Oikealla on myös käytetyt esimerkkikaavat, mutta näiden soluviittaukset riippuvat luonnollisesti datan sijainnista. Omalle välilehdelle kannattaa laittaa osakkeiden hintasarjat, joiden viereen on laskettu tuottosarjat (jotka ovat sijoitusten optimoinnin lähtökohta). Näiden tuottosarjojen perusteella lasketaan tarvittavat riskiluvut. Voit katsoa tästä artikkelista näiden kaavojen laskennasta esimerkkejä.

Varianssi-kovarianssimatriisi

Seuraavaksi tarvitaan varianssi-kovarianssimatriisi. Tämän rakentaminen ei ole sen vaikeampaa kuin varianssin laskeminen, mutta vaatii hieman enemmän työtä. Matriisissa on oltava sama määrä osakkeita pysty- ja vaakarivillä, samassa järjestyksessä. Tässä tapauksessa matriisi on 17 x 17.

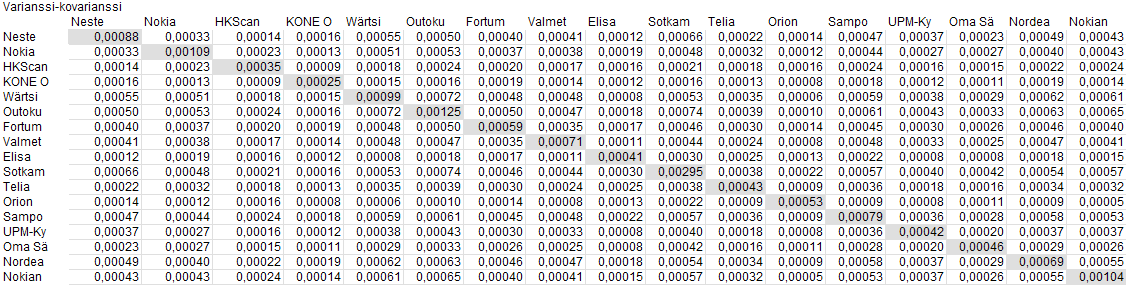
Poikkisoluihin lasketaan varianssi (kuvassa harmaalla), kuten yllä tehtiin tai niihin voi viitata suoraan koska ne ovat jo laskettu. Matriisin muihin soluihin lasketaan kovarianssi excelin KOVARIANSSI -funktiolla, eli jokaiselle osakkeelle tarvitaan kovarianssi muiden salkun osakkeiden tuottojen kanssa.

Kovarianssit tarvitaan varianssien ylä- ja alapuolelle, jotta voimme laskea myöhemmin portfolion varianssin matriisina. Esimerkiksi Nokian ja Nesteen osakkeiden kovarianssi on sama 0,00033 sekä vaaka- että pystyrivillä.

Sijoitussalkun riskiluvut

Seuraavaksi annetaan salkun osakkeille painot, niin että näiden summaksi tulee 100 %. Tässä vaiheessa painojen yksittäisistä arvoista ei tarvitse välittää, koska nämä tullaan optimoimaan. Ne voi jakaa vaikkapa tasan.

Kun painot on annettu, lasketaan salkun odotettu tuotto, joka voidaan laskea osakkeiden tuottojen painotettuna keskiarvona. Tämä onnistuu excelin TULOJEN.SUMMA -funtiolla, jossa toinen sarja on painot ja toinen osakkeiden keskiarvoinen vuosituotto joka laskettiin aiemmin.

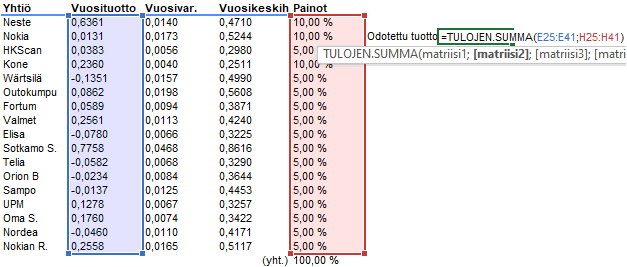
Sijoitussalkun varianssi lasketaan varianssi-kovarianssimatriisista esimerkiksi seuraavalla kaavalla:

{=MKERRO(TRANSPONOI(L3:L19);MKERRO(C47:S63;L3:L19))}

Tässä esimerkissä kaavan L3:L19 soluissa ovat osakkeiden painot ja C47:S63 on varianssi-kovarianssimatriisi. Kaava on matriisikaava, eli se pitää hyväksyä enterin sijaan painamalla Ctrl +Shift + Enter -näppäimiä. Muuten se antaa virhearvon.

Lasketaan vielä keskihajonta ja Sharpen luku. Keskihajonta lasketaan helposti juuri lasketusta salkun varianssista ottamalla siitä neliöjuuri NELIÖJUURI -funktiolla tai korottamalla se ½ eli puolikkaalla.

Sharpen luku lasketaan yksinkertaisesti jakamalla salkun tuotto sen keskihajonnalla, jotka juuri aiemmin laskimme.

Optimaalisen salkun sijoitukset

Edellisissä vaiheissa saimme kaikki tarvittavat luvut. Nyt tarvitsemme excelin ratkaisin -työkalua, joka löytyy työkalupalkin Tiedot-välilehdeltä. Jos tätä ei siellä ole, on se otettava käyttöön asetuksista:

Tiedosto > Asetukset > Apuohjelmat ja valitsemalla alaosasta ”Excel-apuohjelmat” ja painamalla ”Siirry”. Laita merkki ”ratkaisin” -kohtaan ja paina ok.

Ratkaisimessa laitamme tavoitteeksi Sharpen luvun soluviittaus ja valitaan vaihtoehdoista ”Suurin” koska haluamme maksimoida Sharpen, eli millä salkun painokombinaatiolla saamme optimaalisen riski-tuottosuhteen. Laitamme siis vielä ”muuttamalla muuttujasoluja” -kohtaan painot, tässä tapauksessa solut L3-L19).

Ratkaisimessa on laitettava vielä reunaehdot. Syötetään ehdoksi, että painojen summan on oltava 100 %. Tikataan vielä ruutu, ettemme hyväksy negatiivisia painoja (eli emme halua myydä lyhyeksi).

Valinnan mukaan, jos vielä halutaan varmistaa riittävä hajautus, niin rajoitteeksi voidaan vielä syöttää kullekin osakkeelle yläraja, esimerkiksi 20 % mutta tämä on valinnaista (jätämme tämän esimerkissä antamatta). Optimi lasketaan kaikkien annettujen rajoitteiden mukaan.

Lopulta olemme saaneet esimerkkidatan perusteella optimaalisen portfolion, joka sisältää:

Nestettä 46,0 %

Konetta 44,2 %

Sotkamo Silveriä 9,8 %

Sharpen luku on maksimoituna 1,48, portfolion tuotto 47,2 % ja keskihajonta 31,8 %. Nämä kolme ovat myös nousseet salkun osakkeista eniten, samalla kun riski on pysynyt vielä maltillisena ainakin suhteessa muihin salkun osakkeisiin.

Täytyy muistaa, että vuosi 2020 oli hyvin poikkeuksellinen, joten myös optimaalinen salkku on aika poikkeuksellinen ja tässä tapauksessa suosii eniten nousseita osakkeita, eikä tarjoa juurikaan hajautusta ilman ylimääräisiä reunaehtoja.

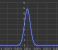
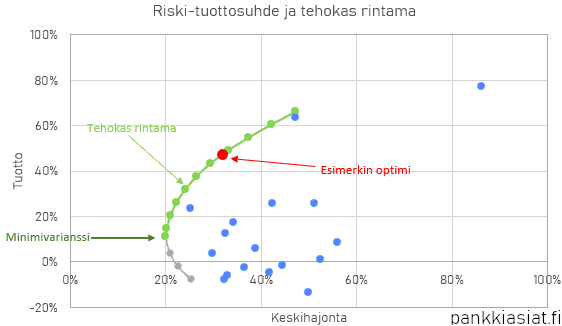Laskemamme optimaalinen riski-tuotto (kuvassa punainen piste) sijoittuu portfolioteorian mukaisesti ns. tehokkaalle rintamalle (kuvassa vihreä käyrän osuus), eli missä sijaitsevat kaikki optimaaliset portfoliot.

Omista riski-tuottomieltymyksistä riippuen, optimaalinen salkku voi liikkua rintamalla. Rajoitteita voi asettaa keskihajonnalle, painoille tai tuotollekin.

Data kannattaa myös valita niin, ettei se sisällä kovin poikkeuksellisia markkinatapahtumia jotka vaikeuttavat tulkintaa. Datan pitäisi kuvata arvopaperin tavanomaista liikkumista ja tuottoa.

Jos haettaisiin alhaisinta riskiä, puhutaan käytännössä tehokkaan rintaman ”kärjestä” eli pienimmän varianssin portfoliosta (minimum variance portfolio). Tämän voi suorittaa samoin ratkaisimessa minimoimalla aiemmin laskettu keskihajonta Sharpen maksimin sijaan. Näin ratkaisu sisältää enemmän osakkeita.

Kuvan siniset pisteet ovat salkun yksittäisten osakkeiden riski-tuottosuhteita. Portfolioteorian mukaisesti voimme havaita, että hajauttamalla ja optimoimalla tuotto-riskisuhteen, päästään parempaan tuottoon alhaisemmalla riskillä.

Voit myös ladata artikkelissa käytetyn excel-pohjan tästä linkistä, mutta käyttäjän on itse muokattava sitä omiin sijoituksiin sopivaksi.

Lue myös:

Sijoituksen tuoton laskeminen

Osakkeen hintahistoria tuoton ja riskin selittäjänä

Sijoittajan hyödylliset excel-kaavat