Tehokkaalla rintamalla (efficient frontier) tarkoitetaan optimaalisten portolioiden, tai "sijoitussalkkujen" mukaista järjestynyttä joukkoa. Tehokas rintama on riski-tuottosuhteen mukaan piirretty käyrä, jossa suurin mahdollinen tuotto vastaa optimaalista tai haluttua riskitasoa. Tehokas rintama ja optimaalinen sijoitusportfolio ovat modernin portfolioteorian ydintä.
Tehokkaan rintaman oikealla puolella sijaitsevat riski-tuottosuhteet, kuten yksittäiset osakkeet, eivät ole optimaalisia. Niissä riskiä on liikaa tuottoa vastaan. Portfolioteorian mukaan riskiä suosivat sijoittajat poimivat pisteen käyrän oikealta puolelta. Riskiä välttävät sijoittajat etsivät pistettä käyrän vasemmalta puolelta, mutta tuotto on siellä vaatimatonta ja ylituottoihin on vaikea päästä.
Tehokasta rintama osoittaa, kuinka sijoitusten hajauttaminen parantaa riski-tuottosuhdetta ja näyttää, ettei riskin ja tuoton suhde ole lineaarinen. Yleensä vain hajauttamalla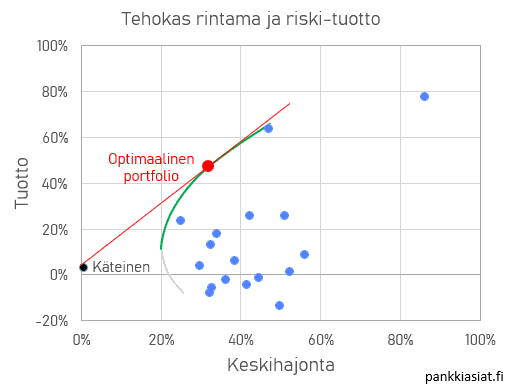 
päästään tehokkaan rintaman käyrälle, vaikka joskus jotkin yksittäiset osakkeet voivat olla sen tuntumassa.
Riski ja tuotto
Portfolion riskimittarina käytetään varianssia tai keskihajontaa, eli volatiliteettia. Tuotto on odotettu tuotto, joka lasketaan yksittäisten tuottojen painotettuna keskiarvona. Portfolion varianssin laskemiseen tarvitaan myös kovarianssi, eli salkun arvopapereiden suhteellinen liikesuunta.
Optimaalinen riski-tuottosuhde on tehokkaan rintaman tangentin (kuvassa punainen viiva) kulmakerroin, jonka päätepiste on kaikista vähäriskisimmässä sijoituksessa. Vähäriskisimmäksi voidaan ajatella käteinen raha, vaikka sekin sisältää pienen määrän riskiä.
Kuvassa siniset pisteet ovat yksittäisiä osakkeita. Tehokas rintama on vihreä käyrä. Käyrä jatkuu harmaana alaoikealle, joka kertoo että heikoimmat sijoitukset ovat sellaisia, joissa riskiä on paljon heikkoa tuottoa vastaan. Rationaalinen sijoittaja valitsee samalla riskitasolla korkeamman tuoton vihreän käyrän kohdalta.
Pienimmän varianssin, eli pienimmän riskin portfolio sijaitsee vihreän ja harmaan käyrän murroskohdassa. Tätä sanotaan myös tehokkaan rintaman kärjeksi.
Tehokkaan rintaman rajoitteet
Tehokkaan rintaman teoria nojaa useisiin oletuksiin, jotka eivät välttämättä heijasta hyvin todellisuutta.
- Sijoittajien oletetaan käyttäytyvän rationaalisesti
- Sijoittajilla oletetaan olevan sama pääsy samaan markkinainformaatioon
- Yksittäinen sijoittaja ei voi vaikuttaa markkinahintoihin
- Kaikki sijoittajat välttävät riskiä ja heillä on sama tuottojen maksimointitavoite
- Kaikilla sijoittajilla on pääsy rajoittamattomaan rahoitukseen riskittömällä korolla
- Tuotot noudattavat normaalijakaumaa
- Sijoittajat nojaavat päätöksissään odotettuihin tuottoihin ja keskihajontaan riskimittarina
Edellä olevien näkökulmien todellisuus riippuu paljolti sijoituskohteesta tai markkinasta. Jossakin ne voivat pitää pääosin paikkaansa, jossakin taas vähemmän. Kuitenkin jos sijoittajia on paljon ja markkinat toimivat vapaasti, voidaan oletusten odottaa keskimäärin toimivan hyvin.
Tehokkaan rintaman laskenta
Koko tehokkaan rintaman laskenta vaatii useita välivaiheita, mikä ei sinänsä ole tarpeellista portfolion optimoinnin kannalta. Valituista sijoituskohteista optimaalisin portfolio saadaan laskemalla ja maksimoimalla Sharpen luku. Pienimmän varianssin portfolio saadaan minimoimalla portfolion keskihajonta.
Näiden laskennasta voi lukea lisää artikkelissa sijoitussalkun optimointi. Itse tehokkaan rintaman käyrän laskeminen onnistuu myös excel -ohjelmalla, mikä voi olla työlästä jos sijoituskohteita on on salkussa useita. Tätä tarkoitusta varten kehitetyt valmisohjelmat tai koodit voivat olla kätevämpiä.
Käytännössä excelissä laskenta onnistuu, mutta vaatii useita ratkaisimen tuottorajoitteiden käyttämistä. Seurataan alkuvaiheissa "sijoitussalkun optimointi" -artikkelia aina siihen, kun portfolion keskihajonta ja tuotto ovat laskettu. Tämän jälkeen portfoliosta valitaan ensin pienimmän ja suurimman odotetun tuoton sijoituskohteet. Niiden väliin interpoloidaan lineaarisesti tuottoja; määräksi on hyvä valita mahdollisimman monta jotta käyrä piirtyy tasaisesti, mutta muutama riittää.
Näitä interpoloituja tuottoja käytetään asteittaisina vähimmäisrajoitteena excelin ratkaisimessa, siirtyessä pienimmästä tuotosta suurimpaan. Jokainen ratkaisun keskihajonta kopioidaan talteen numeroina, eli "mikä on portfolion riski tällä vähimmäistuotolla". Tallennetun keskihajonnan vastinpari on sen interpoloitu tuottorajoite, eli tuotto on y ja keskihajonta x. Näin esimerkiksi 10 ratkaisun jälkeen saadaan riittävästi riski-tuottopareja piirtämään tehokas rintama excelin pistekaaviona.